已知一个口袋中装有 个红球(
个红球( 且
且 )和
)和 个白球,从中有放回地连续摸三次,每次摸出两个球,若两个球颜色不同则为中奖,否则不中奖.
个白球,从中有放回地连续摸三次,每次摸出两个球,若两个球颜色不同则为中奖,否则不中奖.
(1)当 时,设三次摸球中(每次摸球后放回)中奖的次数为
时,设三次摸球中(每次摸球后放回)中奖的次数为 ,求的
,求的 分布列;
分布列;
(2)记三次摸球中(每次摸球后放回)恰有两次中奖的概率为 ,当
,当 取多少时,
取多少时, 最大.
最大.
一射击测试每人射击二次,甲每击中目标一次记10分,没有击中记0分,每次击中目标的概率为 ;乙每击中目标一次记20分,没有击中记0分,每次击中目标的概率为
;乙每击中目标一次记20分,没有击中记0分,每次击中目标的概率为 .
.
(Ⅰ)求甲得10分的概率;
(Ⅱ)求甲乙两人得分相同的概率.
乒乓球单打比赛在甲、乙两名运动员间进行,比赛采用 局
局 胜制(即先胜
胜制(即先胜 局者获胜,比赛结束),假设两人在每一局比赛中获胜的可能性相同,那么甲以
局者获胜,比赛结束),假设两人在每一局比赛中获胜的可能性相同,那么甲以 比2获胜的概率为( )
比2获胜的概率为( )
A. |
B. |
C. |
D. |
口袋内放有大小相同的2个红球和1个白球,有放回地每次摸取一个球,定义数列{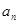 }为
}为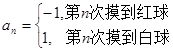 .如果
.如果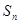 为数列{
为数列{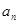 }的前
}的前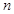 项和,那么
项和,那么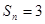 的概率为 ( )
的概率为 ( )
A.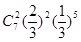 |
B. |
C.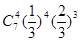 |
D.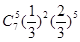 |
5名工人独立地工作,假定每名工人在1小时内平均12分钟需要电力(即任一时刻需要电力的概率为12/60)
(1)设X为某一时刻需要电力的工人数,求 X的分布列及期望;
(2)如果同一时刻最多能提供3名工人需要的电力,求电力超负荷的概率,并解释实际意义.
随机变量ξ的概率分布列为P(ξ=n)=a( )n(n=0.1.2),其中a为常数,列P(0.1<ξ<2.9)的值为
)n(n=0.1.2),其中a为常数,列P(0.1<ξ<2.9)的值为
A. . . |
B. |
C. |
D. |
某次乒乓球比赛的决赛在甲乙两名选手之间举行,比赛采用五局三胜制,决出胜负即停止比赛。按以往的比赛经验,每局比赛中,甲胜乙的概率为 。
。
(1)求比赛三局甲获胜的概率;
(2)求甲获胜的概率;
(3)设比赛的局数为X,求X的分布列和数学期望。
(本小题满分10分)
假定某人每次射击命中目标的概率均为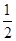 ,现在连续射击3次。
,现在连续射击3次。
(1) 求此人至少命中目标2次的概率;
(2) 若此人前3次射击都没有命中目标,再补射一次后结束射击;否则。射击结束。记此人射击结束时命中目标的次数为X,求X的数学期望。