一射击测试每人射击二次，甲每击中目标一次记10分，没有击中记0分，每次击中目标的概率为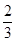
；乙每击中目标一次记20分，没有击中记0分，每次击中目标的概率为
.
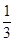（Ⅰ）求甲得10分的概率；
（Ⅱ）求甲乙两人得分相同的概率.
，集合
.
，求
解析式。
，且
时的最小值为
，求实数
的值。
的奇偶性
上单调递增
：对
，
恒成立。
：函数
在
上单调递增。
”为真命题，“
”也为真命题，求实数
的取值范围。
，集合
时，求
,求实数
的取值范围
时，求
的值域
的不等式：
相关知识点
推荐套卷
一射击测试每人射击二次，甲每击中目标一次记10分，没有击中记0分，每次击中目标的概率为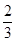；乙每击中目标一次记20分，没有击中记0分，每次击中目标的概率为.
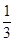（Ⅰ）求甲得10分的概率；
（Ⅱ）求甲乙两人得分相同的概率.
粤公网安备 44130202000953号