任意确定四个日期,其中至少有两个是星期天的概率为________.
乒乓球比赛采用7局4胜制,若甲、乙两人实力相当,获胜的概率各占一半,则打完5局后仍不能结束比赛的概率等于_____________________.
小王通过英语听力测试的概率是 ,他连续测试3次,那么其中恰有1次获得通过的概率是 。
,他连续测试3次,那么其中恰有1次获得通过的概率是 。
投掷两个骰子,至少有一个4点或5点出现时,就说这次试验成功,则在10次试验中,成功次数X的期望是________.
设50件商品中有15件一等品,其余为二等品.现从中随机选购2件,则所购2件商品中恰有一件一等品的概率为________.
箱中装有标号为1,2,3,4,5,6且大小相同的6个球,从箱中一次摸出两个球,记下号码并放回,如果两球号码之积是4的倍数,则获奖.现有4人参与摸奖,恰好有3人获奖的概率是________________.
为了研究性别不同的高中学生是否爱好某项运动,运用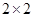 列联表进行独立性检验,经计算
列联表进行独立性检验,经计算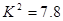 ,则所得到的统计学结论是:有______的把握认为“爱好该项运动与性别有关”.附:
,则所得到的统计学结论是:有______的把握认为“爱好该项运动与性别有关”.附:
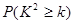 |
0.050 |
0.010 |
0.001 |
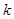 |
3.841 |
6.635 |
10.828 |
某射手每次射击击中目标的概率为P,每次射击的结果相互独立,那么在连续5次射击中,前2次都未击中目标,后3次都击中目标的概率为 .
有20个零件,其中16个一等品,4个二等品,若从这20个零件中任意取3个,那么至少有1个一等品的概率是________.
甲、乙两人进行乒乓球比赛,采用“五局三胜制”,即五局中先胜三局为赢,若每场比赛甲获胜的概率是 ,乙获胜的概率是
,乙获胜的概率是 ,则比赛以甲三胜一负而结束的概率为________.
,则比赛以甲三胜一负而结束的概率为________.