如图,在四棱锥A-BCDE中,侧面∆ADE是等边三角形,底面BCDE是等腰梯形,且CD∥BE,DE=2,CD=4, ,M是DE的中点,F是AC的中点,且AC=4,
,M是DE的中点,F是AC的中点,且AC=4,
求证:(1)平面ADE⊥平面BCD;
(2)FB∥平面ADE.
如图,三棱锥 中,
中, ,
,

(Ⅰ)求证: ;
;
(Ⅱ)若 ,
, 是
是 的中点,求
的中点,求 与平面
与平面 所成角的正切值
所成角的正切值
如图,在等腰梯形 中,
中, 是梯形的高,
是梯形的高, ,
, ,现将梯形沿
,现将梯形沿 折起,使
折起,使 ,且
,且 ,得一简单组合体
,得一简单组合体 如图所示,已知
如图所示,已知 分别为
分别为 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证: 平面
平面 .
.
已知在四棱锥 中,底面
中,底面 是矩形,
是矩形, 平面
平面 ,
, ,
, ,
, 分别是
分别是 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求二面角 的余弦值.
的余弦值.
如图,四棱锥 的底面是直角梯形,
的底面是直角梯形, ,
, ,
, 和
和 是两个边长为
是两个边长为 的正三角形,
的正三角形, ,
, 为
为 的中点,
的中点, 为
为 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形, ,
,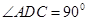 ,平面
,平面 底面
底面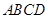 ,
, 为
为 中点,M是棱PC上的点,
中点,M是棱PC上的点,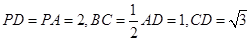 .
.
(1)若点M是棱PC的中点,求证: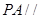 平面
平面 ;
;
(2)求证:平面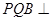 底面
底面 ;
;
(3)若二面角M-BQ-C为 ,设PM=tMC,试确定t的值.
,设PM=tMC,试确定t的值.
若 是两个相交平面, 点
是两个相交平面, 点 不在
不在 内, 也不在
内, 也不在 内, 则过点
内, 则过点 且与
且与 和
和 都平行的直线
都平行的直线
| A.只有1条 | B.只有2条 | C.只有4条 | D.有无数条 |
设  为互不重合的平面,
为互不重合的平面,  是互不重合的直线,给出下列四个命题:
是互不重合的直线,给出下列四个命题:
① 
② 
③ 
④若  ;
;
其中正确命题的序号为 ▲ .
设 为两个不重合的平面,l,m,n为两两不重合的直线,给出下列四个命题:
为两个不重合的平面,l,m,n为两两不重合的直线,给出下列四个命题:
①若
②若
③若
④若m,n是异面直线,
其中真命题的序号是( )
| A.①③④ | B.①②③ | C.①③ | D.②④ |
.若三个平面两两相交,且三条交线互相平行,
则这三个平面把空间分成( )
| A.5部分 | B.6部分 | C.7部分 | D.8部分 |