高中数学误差估计解答题

某高校在2013年的自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组：第1组[160,165），第2组[165,170），第3组[170,175），第4组[175,180），第5组[180,185]，得到的频率分布直方图如图所示．

（1）求第3,4,5组的频率；     
（2）为了了解最优秀学生的情况，该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试，求第3,4,5组每组各抽取多少名学生进入第二轮面试．

某班位学生一次考试数学成绩的频率分布直方图如图，其中成绩分组区间是40,50）, 50,60）, 60,70）,70,80）,80,90）,90,100.若成绩在区间70,90）的人数为34人.
（1）求图中的值及;
（2）由频率分布直方图，求此次考试成绩平均数的估计值.

某班主任对全班50名学生进行了作业量多少的调查．数据如下表：

	认为作业多	认为作业不多	合计
喜欢玩游戏	18	9
不喜欢玩游戏	8	15
合计

（1）请完善上表中所缺的有关数据；
（2）试通过计算说明在犯错误的概率不超过多少的前提下认为喜欢玩游戏与作业量的多少有关系？
附：

P(K^2≥K0)	0.05	0.025	0.010	0.005	0.001
K0	3.841	5.024	6.635	7.879	10.828

某车间共有12名工人，随机抽取6名，他们某日加工零件个数的茎叶图如图所示，其中茎为十位数，叶为个位数.

(1)根据茎叶图计算样本均值；
(2)日加工零件个数大于样本均值的工人为优秀工人．根据茎叶图推断该车间12名工人中有几名优秀工人？
(3)从该车间12名工人中，任取2人，求恰有1名优秀工人的概率．

经销商经销某种农产品，在一个销售季度内，每售出t该产品获利润元，未售出的产品，每t亏损元。根据历史资料，得到销售季度内市场需求量的频率分布直方图，如图所示。经销商为下一个销售季度购进了t该农产品，以（单位：t，）表示下一个销售季度内的市场需求量，(单位：元)表示下一个销售季度内销商该农产品的利润。

（1）将表示为的函数；（2）根据直方图估计利润不少于57000元的概率.

交通指数是交通拥堵指数的简称，是综合反映道路网畅通或拥堵的概念，记交通指数为T．其范围为[0，10]，分别有五个级别：T∈[0，2）畅通;T∈[2，4)基本畅通; T∈[4，6）轻度拥堵; T∈[6，
8)中度拥堵；T∈[8，10]严重拥堵，晚高峰时段，从某市交通指挥中心选取了市区20个交通路段，依据其交通指数数据绘制直方图如图所示．

(1)这20个路段轻度拥堵、中度拥堵的路段各有多少个？
(2)从这20个路段中随机抽出的3个路段，用X表示抽取的中度拥堵的路段的个数，求X的分布列及期望．

由某种设备的使用年限（年）与所支出的维修费（万元）的数据资料，算得，，， ．
（Ⅰ）求所支出的维修费对使用年限的线性回归方程；
（Ⅱ）判断变量与之间是正相关还是负相关；
（Ⅲ）估计使用年限为8年时，支出的维修费约是多少．
附：在线性回归方程中，，，其中，为
样本平均值，线性回归方程也可写为．

某班高一某班的一次数学测试成绩的茎叶图和频率分布图都受到不同程度的破坏，但可见部分如下，据此解答如下问题：
 
(1)求分数在[50,60)的频率及全班人数；
(2)求分数在[80,90)之间的频数，并计算频率分布直方图中[80,90)间的矩形的高；
(3)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况，在抽取的试卷中，求至少有一份分数在[90,100]之间的概率．

成都市为“市中学生知识竞赛”进行选拔性测试，且规定：成绩大于或等于90分的有参赛资格，90分以下（不包括90分）的则被淘汰。若现有500人参加测试，学生成绩的频率分布直方图如下：

（I）求获得参赛资格的人数；
（II）根据频率直方图，估算这500名学生测试的平均成绩；
（III）若知识竞赛分初赛和复赛，在初赛中每人最多有5次选题答题的机会，累计答对3题或答错3题即终止，答对3题者方可参加复赛，已知参赛者甲答对每一个问题的概率都相同，并且相互之间没有影响，已知他连续两次答错的概率为，求甲在初赛中答题个数的分布列及数学期望.

某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩，并用茎叶图记录分数如图所示，但部分数据不小心丢失，同时得到如下所示的频率分布表：

分数段	[50,70)	[70,90)	[90,110)	[110,130)	[130,150)	总计
频数				b
频率	a	0.25

（1）求表中a，b的值及分数在[90,100)范围内的学生人数，并估计这次考试全校学生数学成绩的及格率（分数在[90,150）内为及格）：
（2）从成绩在[100,130)范围内的学生中随机选4人，
设其中成绩在[100,110)内的人数为X，求X的分布列及数学期望.

．
某校从高一年级学生中随机抽取60名学生，将其期中考试的数学成绩（均为整数）分成六段，，…，后得到如下频率分布直方图．
（1）求分数在内的频率；
（2）用分层抽样的方法在80分以上（含80分）的学生中抽取一个容量为6的样本，将该样本看成一个总体，从中任意选取2人，求其中恰有1人的分数不低于90分的概率．

某中学号召学生在今年春节期间至少参加一次社会公益活动（以下简称活动）．该校合唱团共有100名学生，他们参加活动的次数统计如图所示．

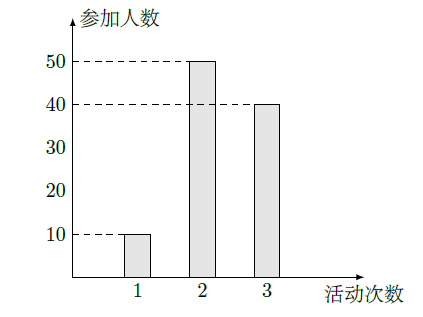
（I）求合唱团学生参加活动的人均次数；
（II）从合唱团中任意选两名学生，求他们参加活动次数恰好相等的概率．
（III）从合唱团中任选两名学生，用 $\xi$ 表示这两人参加活动次数之差的绝对值，求随机变量 $\xi$ 的分布列及数学期望 $E\xi$ ．

为了解学生身高情况，某校以 $10\%$ 的比例对全校 $700$ 名学生按性别进行分层抽样检查，测得身高情况的统计图如下：

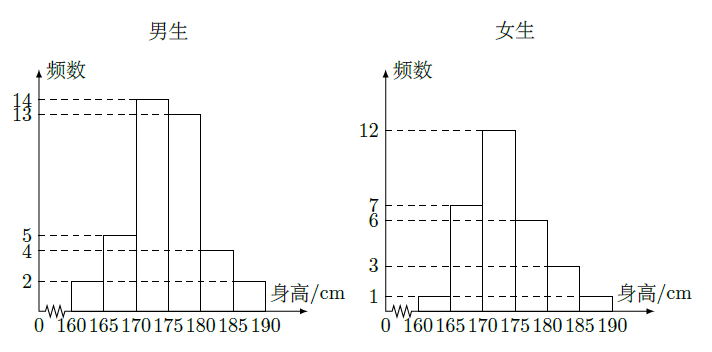
（Ⅰ）估计该校男生的人数；
（Ⅱ）估计该校学生身高在 $170~185cm$ 之间的概率；
（Ⅲ）从样本中身高在 $180~190cm$ 之间的男生中任选 $2$ 人，求至少有 $1$ 人身高在 $185~190cm$ 之间的概率.

对400个某种型号的电子元件进行寿命追踪调查，其频率分布表如下表：

寿命（h）	频率
500600	0.10
600700	0.15
700800	0.40
800900	0.20
9001000	0.15
合计	1

 
（I）在下图中补齐频率分布直方图；
（II）估计元件寿命在500800h以内的概率。

（本小题满分12分）
按照新课程的要求, 高中学生在每学期都要至少参加一次社会实践活动（以下简称活动）．某校高一·一班50名学生在上学期参加活动的次数统计如条形图所示．

（Ⅰ）求该班学生参加活动的人均次数；
（Ⅱ）从该班中任意选两名学生，求他们参加活动次数恰好相等的概率；
（Ⅲ）从该班中任选两名学生，用表示这两人参加活动次数之差的绝对值，求随机变量的分布列及数学期望．（要求：答案用最简分数表示）