高中数学误差估计解答题

从某企业生产的某种产品中抽取100件，测量这些产品的一项质量指标值，由测量表得如下频数分布表：

质量指标值分组	[75，85）	[85，95）	[95，105）	[105，115）	[115，125）
频数	4	16	40	32	8

（1）在答题卡上作出这些数据的频率分布直方图；（用阴影涂黑）

（2）估计这种产品质量指标值的平均数及中位数；
（3）根据以上抽样调查数据，能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的75%”的规定？

医生的专业能力参数可有效衡量医生的综合能力，越大，综合能力越强，并规定: 能力参数不少于30称为合格，不少于50称为优秀．某市卫生管理部门随机抽取300名医生进行专业能力参数考核，得到如图所示的能力的频率分布直方图:

（Ⅰ）求出这个样本的合格率、优秀率；
（Ⅱ）现用分层抽样的方法从中抽出一个样本容量为20的样本，再从这20名医生中随机选出2名．
①求这2名医生的能力参数为同一组的概率；
②设这2名医生中能力参数为优秀的人数为，求随机变量的分布列和期望．

从参加环保知识竞赛的学生中抽出60名,将其成绩整理后画出的频率分布直方图如下．观察图形，回答下列问题：

（1）49．5——69．5这一组的频率和频数分别为多少?
（2）估计这次环保知识竞赛成绩的中位数及平均成绩．（精确到小数点后一位）

某班50名学生在一次数学测试中，成绩全部介于50与100之间，将测试结果按如下方式分成五组：第一组[50，60），第二组[60，70），…，第五组[90，100]．如图所示是按上述分组方法得到的频率分布直方图．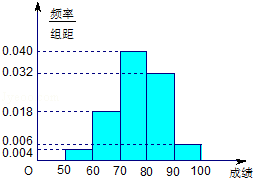

（Ⅰ）若成绩大于或等于60且小于80，认为合格，求该班在这次数学测试中成绩合格的人数；
（Ⅱ）从测试成绩在[50，60）∪[90，100]内的所有学生中随机抽取两名同学，设其测试成绩分别为m、n，求事件“|m﹣n|＞10”概率．

某校高二某班的一次数学测试成绩（满分为分）的茎叶图和频率分布直方图都受到不同程度的破坏，但可见部分如下，据此解答如下问题：

（1）求分数在的频率及全班人数；
（2）求分数在之间的频数，并计算频率分布直方图中间的矩形的高；
（3）若要从分数在 之间的试卷中任取两份分析学生失分情况，在抽取的试卷中，求至少有一份分数在之间的概率．

（本小题满分13分）某超市从2014年甲、乙两种酸奶的日销售量（单位：箱）的数据中分别随机抽取100个，整理得到数据分组及频率分布表和频率分布直方图： 

分组（日销售量）	频率（甲种酸奶）
[ 0，10]	0．10
（10，20]	0．20
（20，30]	0．30
（30，40]	0．25
（40，50]	0．15

 

（Ⅰ）写出频率分布直方图中的的值，并作出甲种酸奶日销售量的频率分布直方图；

（Ⅱ）记甲种酸奶与乙种酸奶日销售量（单位：箱）的方差分别为，，试比较与的大小；（只需写出结论）
（Ⅲ）假设同一组中的每个数据可用该组区间的中点值代替,试估计乙种酸奶在未来一个月（按30天计算）的销售总量．

甲、乙两位学生参加数学竞赛培训，现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次，记录如下：
甲  82  81  79  78  95  88  93  84
乙  92  95  80  75  83  80  90  85
（1）用茎叶图表示这两组数据；
（2）现要从中选派一人参加数学竞赛，从统计学的角度（在平均数、方差或标准差中选两个）分析，你认为选派哪位学生参加合适？请说明理由
参考公式：

在一次考试中，5名同学数学、物理成绩如下表所示：

学生	A	B	C	D	E
数学（x分）	89	91	93	95	97
物理（y分）	87	89	89	92	93

 
（1）根据表中数据，求物理分对数学分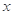的回归方程：
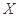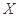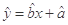（2）要从4名数学成绩在90分以上的同学中选出2名参加一项活动，以表示选中的同学中物理成绩高于90分的人数，求随机变量的分布列及数学期望．（附：回归方程中，，）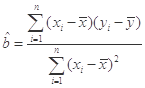

我国政府对PM2.5采用如下标准：

PM2.5日均值m（微克/立方米）	空气质量等级
	一级
	二级
	超标

某市环保局从一年365天的市区PM2.5监测数据中，随机抽取10天的数据作为样本，监测值如茎叶图所
示（十位为茎，个位为叶）．

树茎	树叶
2	8 2
3	8 2 1
4	4 5
6	3 8
7	7

（1）求这10天数据的中位数；
（2）从这10天数据中任取4天的数据，记为空气质量达到一级的天数，求的分布列和期望；
（3）以这10天的数据来估计这一年365天的空气质量情况，并假定每天之间的空气质量相互不影响．记
为这一年中空气质量达到一级的天数，求的平均值．

为了检测某种产品的质量，抽取了一个容量为100的样本，数据的分组数如下：
；；；；；；； ； ；
（1）完成频率分布表，并画出频率分布直方图以及频率分布折线图；
（2）据上述图表，估计数据落在范围内的可能性是百分之几？
（3）数据小于11．20的可能性是百分之几？

国家环境标准制定的空气质量指数与空气质量等级对应关系如下表：

由全国重点城市环境监测网获得2月份某五天甲城市和乙城市的空气质量指数数据用茎叶图表示如图：

（Ⅰ）试根据上面的统计数据，判断甲、乙两个城市的空气质量指数的方差的大小关系（只需写出结果）；
（Ⅱ）试根据上面的统计数据，估计甲城市某一天空气质量等级为2级良的概率；
（Ⅲ）分别从甲城市和乙城市的统计数据中任取一个，试求这两个城市空气质量等级相同的概率．
（注：s²=[（x₁﹣）²+（x₂﹣）²+…+（x_n﹣）²]，其中为数据x₁，x₂，…，x_n的平均数．）

某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50,60），[60,70），[70,80），[80,90），[90,100]．

（1）求图中a的值；
（2）根据频率分布直方图，估计这100名学生语文成绩的平均分；
（3）若这100名学生语文成绩某些分数段的人数（x）与数学成绩相应分数段的人数（y）之比如下表所示，
求数学成绩在[50,90）之外的人数．

分数段	[50,60）	[60, 70）	[70,80）	[80,90）
x∶y	1∶1	2∶1	3∶4	4∶5

 

某班50名学生在一次百米测试中，成绩全部介于13秒与18秒之间，将测试结果按如下方式分成五组：第一组，第二组， ，第五组.下图是按上述分组方法得到的频率分布直方图.按上述分组方法得到的频率分布直方图.

（Ⅰ）若成绩大于或等于14秒且小于16秒认为良好，求该班在这次百米测试中成绩良好的人数；
（Ⅱ）设m,n表示该班某两位同学的百米测试成绩，且已知求事件“”发生的概率.

某校联合社团有高一学生126人，高二学生105人，高三学生42人，现
用分层抽样的方法从中抽取13人进行关于社团活动的问卷调查．设问题的选择分为“赞同”和“不赞同”两种，且每人都做出了一种选择．下面表格中提供了被调查学生答卷情况的部分信息．
（1）完成下列统计表：

（2）估计联合社团的学生中“赞同”的人数；
（3）从被调查的高二学生中选取2人进行访谈，求选到的两名学生中恰好有一人“赞同”的概率．

（本小题满分12分）
某校从参加高二年级期中考试的学生中随机抽取名学生，将其数学成绩（均为整数）分成六段，…后得到如下部分频率分布直方图，观察图形的信息，回答下列问题：

（1）求分数在内的频率，并补全这个频率分布直方图；
（2）根据频率分布直方图，估计本次数学成绩的平均数；
（3）用分层抽样的方法在分数段为的学生中抽取一个容量为的样本，将该样本看成一个总体，从中任取人，求恰好有人分数在的概率．