湖北孝感高中高二上学期期中文科数学试卷
下列反映两个变量的相关关系中,不同于其它三个的是
| A.名师出高徒 | B.水涨船高 | C.月明星稀 | D.登高望远 |
“事件A,B互斥”是“事件A,B对立”的
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
孝感市2014年各月的平均气温( )数据的茎叶图如下:
)数据的茎叶图如下:

则这组数据的中位数是
| A.23 | B.21.5 | C.20 | D.19 |
命题“存在一个无理数,它的平方是有理数”的否定是
| A.任意一个无理数,它的平方不是有理数 |
| B.任意一个有理数,它的平方是有理数 |
| C.存在一个有理数,它的平方是有理数 |
| D.存在一个无理数,它的平方不是有理数 |
执行如图所示的程序框图,如果输出 ,那么判断框内应填入的条件是
,那么判断框内应填入的条件是
| A.k≤6 | B.k≤7 | C.k≤8 | D.k≤9 |
已知具有线性相关的两个变量x,y之间的一组数据如下:
 |
0 |
1 |
2 |
3 |
4 |
 |
2.2 |
4.3 |
t |
4.8 |
6.7 |
且回归方程是 ,则t=
,则t=
A.4.7 B.4.6 C.4.5 D.4.4
下列关于概率的理解中正确的命题的个数是
①掷10次硬币出现4次正面,所以掷硬币出现正面的概率是0.4;
②某种体育彩票的中奖概率为 ,则买1000张这种彩票一定能中奖;
,则买1000张这种彩票一定能中奖;
③孝感气象台预报明天孝感降雨的概率为70%是指明天孝感有70%的区域下雨,30%的区域不下雨.
| A.0 | B.1 | C.2 | D.3 |
下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入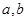 分别为14,18,则输出的
分别为14,18,则输出的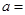
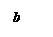
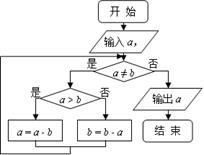
| A.0 | B.2 | C.4 | D.14 |
对任意的实数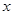 ,若
,若 表示不超过
表示不超过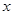 的最大整数,则“
的最大整数,则“ ”是“
”是“ ”的
”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
对于两随机事件A,B若 ,则事件A,B的关系是
,则事件A,B的关系是
| A.互斥且对立 | B.互斥不对立 |
| C.既不互斥也不对立 | D.以上均有可能 |
一个路口的红绿灯,红灯的时间是30秒,黄灯的时间是5秒,绿灯的时间是40秒,当你到达路口时遇见红灯的概率是 .
在一次射击训练中,某战士连续射击了两次.设命题 是“第一次射击击中目标”,
是“第一次射击击中目标”,  是“第二次射击击中目标”.则命题“两次都没有击中目标”用
是“第二次射击击中目标”.则命题“两次都没有击中目标”用 ,
, 及逻辑联结词可以表示为 .
及逻辑联结词可以表示为 .
在下列给出的命题中,所有正确命题的序号为 .
①若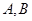 为互斥事件,则
为互斥事件,则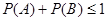 ;
;
②若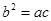 ,则
,则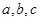 成等比数列;
成等比数列;
③经过两个不同的点 、
、 的直线都可以用方程
的直线都可以用方程
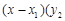
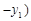 来表示;
来表示;
④若函数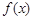 对一切
对一切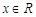 满足:
满足: ,则函数
,则函数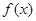 为奇函数或偶函数;
为奇函数或偶函数;
⑤若函数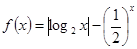 有两个不同的零点
有两个不同的零点 ,则
,则 .
.
海关对同时从 三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如下表所示,工作人员用分层抽样的方法从这些商品中共抽取6件进行检测.
三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如下表所示,工作人员用分层抽样的方法从这些商品中共抽取6件进行检测.
| 地区 |
 |
 |
 |
| 数量 |
50 |
150 |
100 |
(1)求这6件样品中来自 各地区商品的数量;
各地区商品的数量;
(2)若在这6件样品中随机抽取2件送往甲机构进一步检测,求这2件商品来自相同地区的概率.
 的取值范围为[0,10],给出如图所示程序框图,输入一个数
的取值范围为[0,10],给出如图所示程序框图,输入一个数 .
.
(1)请写出程序框图所表示的函数表达式;
(2)求输出的 (
( )的概率;(3)求输出的
)的概率;(3)求输出的 的概率.
的概率.
从参加环保知识竞赛的学生中抽出60名,将其成绩整理后画出的频率分布直方图如下.观察图形,回答下列问题:
(1)49.5——69.5这一组的频率和频数分别为多少?
(2)估计这次环保知识竞赛成绩的中位数及平均成绩.(精确到小数点后一位)
(1)已知

 ,
,
 .若“
.若“ ”是“
”是“ ”的充分不必要条件,求实数
”的充分不必要条件,求实数 的取值范围;
的取值范围;
(2)已知两个关于x的一元二次方程mx2-4x+4=0和x2-4mx+4m2-4m-5=0,求两方程的根都是整数的充要条件.
设有关于x的一元二次方程 .
.
(1)若 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数, 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率.
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率.
(2)若 是从区间
是从区间 任取得一个数,
任取得一个数, 是从区间
是从区间 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.
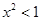 ,则
,则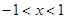 的逆否命题是
的逆否命题是 ,则
,则 或
或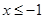
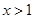 或
或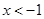 ,则
,则

 与
与 的图象上存在关于
的图象上存在关于 轴对称的点,则实数
轴对称的点,则实数 的取值范围是
的取值范围是



 ”是真命题,则实数
”是真命题,则实数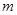 的最小值为 .
的最小值为 . 为定义域D上的单调函数,且存在区间
为定义域D上的单调函数,且存在区间 ,使得当
,使得当 时,函数
时,函数 ,则称函数
,则称函数 上的“正函数”,区间
上的“正函数”,区间 是否为“正函数”?若是“正函数”,求函数
是否为“正函数”?若是“正函数”,求函数 的“正区间”;若不是“正函数”,请说明理由;
的“正区间”;若不是“正函数”,请说明理由; :
: 是“正函数”;命题
是“正函数”;命题 :
: 是“正函数”.若
是“正函数”.若 是真命题,求实数
是真命题,求实数 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号