高中数学误差估计解答题

（本小题满分10分） 从甲、乙两名学生中选拔一人参加射箭比赛，为此需要对他们的射箭水平进行测试．现这两名学生在相同条件下各射箭10次，命中的环数如下：

甲	8	9	7	9	7	6	10	10	8	6
乙	10	9	8	6	8	7	9	7	8	8

 
（1）计算甲、乙两人射箭命中环数的平均数和标准差；
（2）比较两个人的成绩，然后决定选择哪名学生参加射箭比赛．

为了参加奥运会，对自行车运动员甲、乙两人在相同的条件下进行了6次测试，测得他们的最大速度的数据如表所示：

甲	27	38	30	37	35	31
乙	33	29	38	34	28	36

 
（1）分别求甲、乙两运动员最大速度
的平均数，及方差，；
（2）根据（1）所得数据阐明：谁参加这项重 大比赛更合适．

（本小题满分12分）对甲､乙的学习成绩进行抽样分析,各抽5门功课,得到的观测值如下

甲	60	80	70	90	70
乙	80	60	70	80	75

问:甲､乙两人谁的平均成绩高?谁的各门功课发展较平衡? 

（本小题满分12分）某单位对三个车间的人数统计情况如下表:用分层抽样的方法从三个车间抽取30人，其中三车间有12人．

	一车间	二车间	三车间
男职工	200	100	250
女职工	600		550

 
（Ⅰ）求的值；
（Ⅱ）为了考察职工加班情况，从编号000～199中的一车间男职工中，用系统抽样法先后抽取5人的全年加班天数分别为75，79，82，73，81．已知73对应的编号为145，75对应的编号是多少?并求这五个人加班天数的方差．

（本小题满分12分）某城市户居民的月平均用电量（单位：度），以，，，，，，分组的频率分布直方图如图．

（1）求直方图中的值；
（2）求月平均用电量的众数和中位数；
（3）在月平均用电量为，，，的四组用户中，用分层抽样的方法抽取户居民，则月平均用电量在的用户中应抽取多少户？

（本小题满分8分）从某校高一年级800名学生中随机抽取100名测量身高，测量后发现被抽取的学生身高全部介于155厘米和195厘米之间，将测量结果分为八组：第一组，第二组，……，第八组，得到频率分布直方图如右．

（Ⅰ）计算第七组[185，190）的样本数；并估计这个高一年级800名学生中身高在170厘米以下的人数；
（Ⅱ） 求出这100名学生身高的中位数、平均数．

甲、乙两同学的6次考试成绩分别为:

甲
乙

 
（Ⅰ）画出甲、乙两同学6次考试成绩的茎叶图；
（Ⅱ）计算甲、乙两同学考试成绩的方差，并对甲、乙两同学的考试成绩做出合理评价．

（本小题满分12分）某学校1800名学生在一次百米测试中，成绩全部介于13秒与18秒之间，抽取其中50个样本，将测试结果按如下方式分成五组：第一组，第二组，…，第五组，下图是按上述分组方法得到的频率分布直方图．

（1）若成绩小于15秒认为良好，求该样本在这次百米测试中成绩良好的人数；
（2）请估计学校1800名学生中，成绩属于第四组的人数；
（3）请根据频率分布直方图，求样本数据的众数和中位数．

某工厂36名工人年龄数据如图：

（1）用系统抽样法从36名工人中抽取容量为9的样本，且在第一分段里用随机抽样法抽到的年龄数据为44，列出样本的年龄数据；
（2）计算（1）中样本的均值 $\bar{x}$和方差 $s^2$；
（3）36名工人中年龄在 $\bar{x}$﹣ $s$和 $\bar{x}$+ $s$之间有多少人？所占百分比是多少（精确到 $0.01\%$）？

某城市 $100$ 户居民的月平均用电量（单位：度），以 $[160,180)$ ， $[180,200)$ ， $[200,220)$ ， $[220,240)$ ， $[240,260)$ ， $[260,280)$ ， $\left[280,300\right]$ 分组的频率分布直方图如图．

（1）求直方图中 $x$ 的值；
（2）求月平均用电量的众数和中位数；
（3）在月平均用电量为 $[220,240)$ ， $[240,260)$ ， $[260,280)$ ， $\left[280,300\right]$ 的四组用户中，用分层抽样的
方法抽取 户居民，则月平均用电量在 $[220,240)$ 的用户中应抽取多少户？

（本小题满分12分）
已知一组数据的频率分布直方图如下.求(1)众数;(2)中位数;(3)平均数.

为了解甲、乙两厂的产品质量，分别从两厂生产的产品中各随机抽取10件，测量产品中某种元素的含量（单位：毫克），其测量数据的茎叶图如下：

规定：当产品中此种元素含量大于18毫克时，认定该产品为优等品。
（Ⅰ）试比较甲、乙两厂生产的产品中该种元素含量的平均值的大小；
（Ⅱ）现从乙厂抽出的非优等品中随机抽取两件，求至少抽到一件该元素含量为10毫克或13毫克的产品的概率。

（本小题满分12分）下图是某市今年1月份前30天空气质量指数（AQI）的趋势图.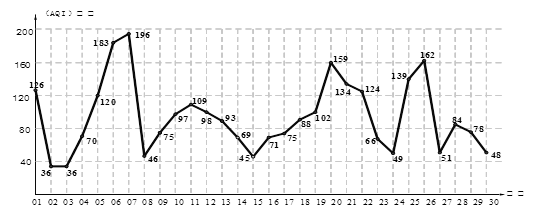

（1）根据该图数据在答题卷中完成频率分布表，并在图中补全这些数据的频率分布直方图；

（2）当空气质量指数（AQI）小于100时，表示空气质量优良．某人随机选择当月（按30天计）某一天
到达该市，根据以上信息，能否认为此人到达当天空气质量优良的可能性超过60%？

（本小题满分12分）为了解甲、乙两厂的产品质量，分别从两厂生产的产品中各随机抽取10件，测量产品中某种元素的含量（单位：毫克），其测量数据的茎叶图如下：

规定:当产品中此种元素含量大于18毫克时，认定该产品为优等品。
（1）试比较甲、乙两厂生产的产品中该种元素含量的平均值的大小；
（2）从乙厂抽出上述10件产品中，随机抽取3件，求抽到的3件产品中优等品数的分布列及数学期望。

（本小题满分13分）从甲、乙两班某项测试成绩中各随机抽取5名同学的成绩，得到如下茎叶图．已知甲班样本成绩的中位数为13, 乙班样本成绩的平均数为16．

（1）求的值；
（2）试估计甲、乙两班在该项测试中整体水平的高低（只需写出结论)；
（3）从两组样本成绩中分别去掉一个最低分和一个最高分，再从两组
剩余成绩中分别随机选取一个成绩，求这两个成绩的和的分布列及数学期望．
（注：方差，其中为，，  ,的平均数．）