某城市
户居民的月平均用电量(单位:度),以
,
,
,
,
,
,
分组的频率分布直方图如图.
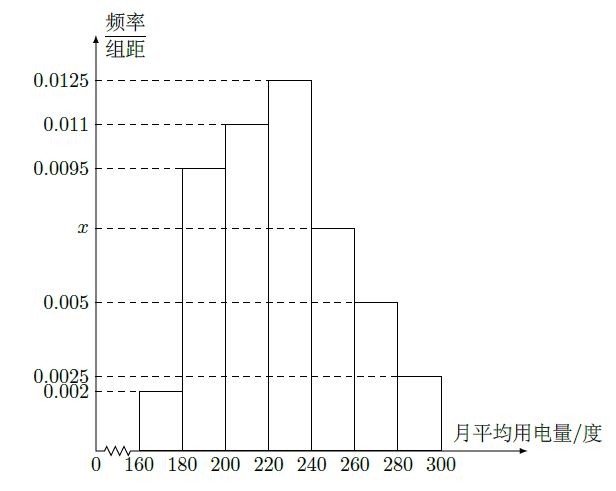
(1)求直方图中
的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为
,
,
,
的四组用户中,用分层抽样的
方法抽取  户居民,则月平均用电量在
的用户中应抽取多少户?
户居民,则月平均用电量在
的用户中应抽取多少户?
相关知识点
推荐套卷
某城市
户居民的月平均用电量(单位:度),以
,
,
,
,
,
,
分组的频率分布直方图如图.

(1)求直方图中
的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为
,
,
,
的四组用户中,用分层抽样的
方法抽取  户居民,则月平均用电量在
的用户中应抽取多少户?
户居民,则月平均用电量在
的用户中应抽取多少户?