为了了解高三学生的数学成绩,抽取了某班60名学生,将所得数据整理后,画出其频率分布直方图(如下图),已知从左到右各长方形高的比为 ,则该班学生数学成绩在
,则该班学生数学成绩在 之间的学生人数是( )
之间的学生人数是( )
| A.32 | B.27 | C.24 | D.33 |
某班级统计一次数学测试后的成绩,并制成了如下的频率分布表,根据该表估计该班级的数学测试平均分为( )
| 分组 |
 |
 |
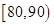 |
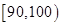 |
| 人数 |
5 |
15 |
20 |
10 |
| 频率 |
0.1 |
0.3 |
0.4 |
0.2 |
(A)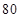 (B)
(B)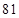 (C)
(C) (D)
(D)
某班级统计一次数学测试后的成绩,并制成了如下的频率分布表,根据该表估计该班级的数学测试平均分为( )
| 分组 |
 |
 |
 |
 |
| 人数 |
5 |
15 |
20 |
10 |
| 频率 |
0.1 |
0.3 |
0.4 |
0.2 |
(A) (B)
(B) (C)
(C) (D)
(D)
数学考试中,甲、乙两校的成绩平均分相同,但甲校的成绩比乙校整齐,若甲、乙两校的成绩方差分别为 和
和 ,则( )
,则( )
A. > > |
B. < < |
C. = = |
D.S1>S2 |
如图是总体密度曲线,下列说法正确的是( )
| A.组距越大,频率分布折线图越接近于它 |
| B.样本容量越小,频率分布折线图越接近于它 |
| C.阴影部分的面积代表总体在(a,b)内取值的百分比 |
| D.阴影部分的平均高度代表总体在(a,b)内取值的百分比 |
已知一组正数x1,x2,x3,x4的方差为s2= ×(
×( +
+ +
+ +
+ -16),则数据x1+2,x2+2,x3+2,x4+2的平均数为( )
-16),则数据x1+2,x2+2,x3+2,x4+2的平均数为( )
| A.2 | B.3 | C.4 | D.6 |
为选拔运动员参加比赛,测得7名选手的身高(单位:cm)分布茎叶图为
记录的平均身高为177cm,有一名候选人的身高记录不清楚,其末位数字记为x,那么x的值为( )
| A.5 | B.6 | C.7 | D.8 |
某校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,结果用如图所示的条形图表示,根据条形图可得这50名学生这一天平均每人的课外阅读时间为( )
| A.0.6h | B.0.9h | C.1.0h | D.1.5h |
10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则有( )
| A.a>b>c | B.b>c>a |
| C.c>a>b | D.c>b>a |
甲、乙两人在一次射击比赛中各射靶5次,两人成绩的条形统计图如图所示,则( )
| A.甲的成绩的平均数小于乙的成绩的平均数 |
| B.甲的成绩的中位数等于乙的成绩的中位数 |
| C.甲的成绩的方差小于乙的成绩的方差 |
| D.甲的成绩的极差小于乙的成绩的极差 |
在样本的频率分布直方图中,共有11个小长方形,若中间一个长方形的面积等于其他10个小长方形面积和的 ,且样本容量为160,则中间一组的频数为( )
,且样本容量为160,则中间一组的频数为( )
| A.32 | B.0.2 |
| C.40 | D.0.25 |
在某次测量中得到的A样本数据如下:82,84,84,86,86,86,88,88,88,88.若B样本数据恰好是A样本数据每个都加2后所得数据.则A,B两样本的下列数字特征对应相同的是( )
| A.众数 | B.平均数 |
| C.中位数 | D.标准差 |
某苗圃基地为了解基地内甲、乙两块地种植的同一种树苗的长势情况,从两块地各随机抽取了10株树苗,用茎叶图表示上述两组数据,对两块地抽取树苗的高度的平均数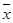 甲、
甲、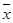 乙和中位数y甲、y乙进行比较,下面结论正确的是( )
乙和中位数y甲、y乙进行比较,下面结论正确的是( )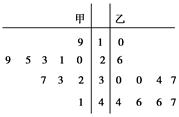
A.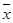 甲> 甲>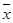 乙,y甲>y乙 乙,y甲>y乙 |
B.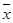 甲< 甲<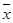 乙,y甲<y乙 乙,y甲<y乙 |
C.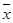 甲< 甲<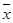 乙,y甲>y乙 乙,y甲>y乙 |
D.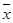 甲> 甲>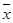 乙,y甲<y乙 乙,y甲<y乙 |
某射击俱乐部四名运动员甲、乙、丙、丁在选拔赛 中所得的平均环数 及其方差
及其方差 如表所示,若从中选送一人参加决赛,则最佳人选是
如表所示,若从中选送一人参加决赛,则最佳人选是
| |
甲 |
乙 |
丙 |
丁 |
 |
9.1 |
9.3 |
9.3 |
9.2 |
 |
5.7 |
6.2 |
5.7 |
6.4 |
A.甲 B.乙
C.丙 D.丁
右图是一容量为 的样本的重量的频率分布直方图,样本重量均在
的样本的重量的频率分布直方图,样本重量均在 内,其分组为
内,其分组为 ,
, ,
, ,则样本重量落在
,则样本重量落在 内的频数为( )
内的频数为( )
A. |
B. |
C. |
D. |