高中数学误差估计试题

某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩，并用茎叶图记录分数如图所示，但部分数据不小心丢失，同时得到如下所示的频率分布表：

分数段	[50,70)	[70,90)	[90,110)	[110,130)	[130,150)	总计
频数				b
频率	a	0.25

（1）求表中a，b的值及分数在[90,100)范围内的学生人数，并估计这次考试全校学生数学成绩的及格率（分数在[90,150）内为及格）：
（2）从成绩在[100,130)范围内的学生中随机选4人，
设其中成绩在[100,110)内的人数为X，求X的分布列及数学期望.

一次选拔运动员，测得7名选手的身高（单位cm）分布茎叶图如图，测得平均身高为177cm，有一名候选人的身高记录不清楚，其末位数记为，那么的值为

A．5

B．6

C．7

D．8

在抽查某产品尺寸过程中，将其尺寸分成若干组，［a，b］是其中一组，已知该组的频率为m，该组上的直方图的高为h，则｜a－b｜等于 (    )

A．mh

B．

C．

D．m+h

．
某校从高一年级学生中随机抽取60名学生，将其期中考试的数学成绩（均为整数）分成六段，，…，后得到如下频率分布直方图．
（1）求分数在内的频率；
（2）用分层抽样的方法在80分以上（含80分）的学生中抽取一个容量为6的样本，将该样本看成一个总体，从中任意选取2人，求其中恰有1人的分数不低于90分的概率．

下列说法正确的是

A．根据样本估计总体，其误差与所选择的样本容量无关

B．方差和标准差具有相同的单位

C．从总体中可以抽取不同的几个样本

D．如果容量相同的两个样本的方差满足S1^2<S2^2，那么推得总体也满足S1^2<S2^2是错的

如果数据，方差是的
平均数和方差分别是    （   ）                           

A．	B．
C．	D．

甲，乙，丙三名运动员在某次测试中各射击20次，三人测试成绩的频率分布条形图分别如图1，图2和图3，若，，分别表示他们测试成绩的标准差，则

A．	B．
C．	D．

某中学号召学生在今年春节期间至少参加一次社会公益活动（以下简称活动）．该校合唱团共有100名学生，他们参加活动的次数统计如图所示．

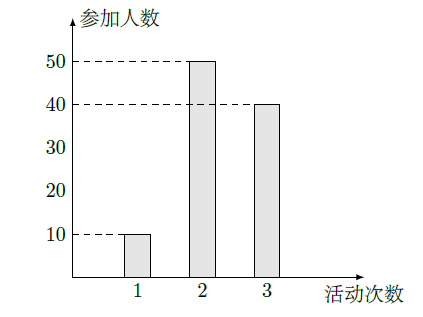
（I）求合唱团学生参加活动的人均次数；
（II）从合唱团中任意选两名学生，求他们参加活动次数恰好相等的概率．
（III）从合唱团中任选两名学生，用 $\xi$ 表示这两人参加活动次数之差的绝对值，求随机变量 $\xi$ 的分布列及数学期望 $E\xi$ ．

在某项体育比赛中一位同学被评委所打出的分数如下：
90     89    90   95   93   94   93
去掉一个最高分和一个最低分后，所剩数据的平均分值为和方差分别为

A．	92，2	B．	92，2.8
C．	93，2	D．	93，2.8

为了解学生身高情况，某校以 $10\%$ 的比例对全校 $700$ 名学生按性别进行分层抽样检查，测得身高情况的统计图如下：

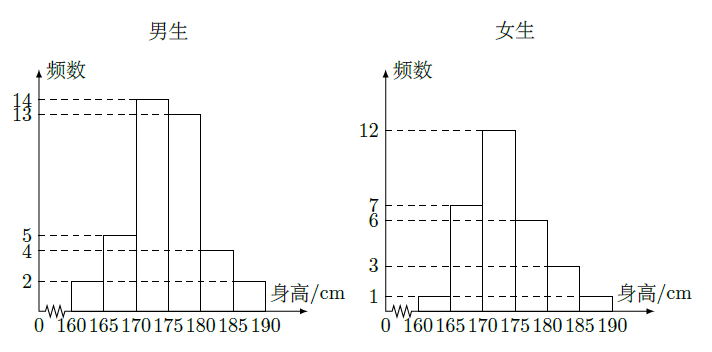
（Ⅰ）估计该校男生的人数；
（Ⅱ）估计该校学生身高在 $170~185cm$ 之间的概率；
（Ⅲ）从样本中身高在 $180~190cm$ 之间的男生中任选 $2$ 人，求至少有 $1$ 人身高在 $185~190cm$ 之间的概率.

从某小学随机抽取100名同学，将他们的身高（单位：厘米）数据绘制成频率分布直方图（如图）。由图中数据可知 $a＝$ .若要从身高在[120,130）,[130，140) , [140,150]三组内的学生中，用分层抽样的方法选取18人参加一项活动，则从身高在[140150]内的学生中选取的人数应为 .

某棉纺厂为了了解一批棉花的质量，从中随机抽取了100根棉花纤维的长度（棉花纤维的长度是棉花质量的重要指标），所得数据都在区间 $\left[5,40\right]$ 中，其频率分布直方图如图所示，则其抽样的100根中，有 根在棉花纤维的长度小于20 $mm$ 。

一个社会调查机构就某地居民的月收入调查了10000人，并根据所得数据画了样本的频率分布直方图（如右图）。为了分析居民的收入与年龄、学历、职业等方面的关系，每隔500元一段要从这10000人中再用分层抽样方法抽出100人作进一步调查，则在［2500，3000）（元）月收入段应抽出的人数为 （   ）

A．20

B．25

C．35

D．45

已知三个正态分布密度函数（，）的图象如下所示，则（  ）

A．，

B．，

C．，

D．，

对400个某种型号的电子元件进行寿命追踪调查，其频率分布表如下表：

寿命（h）	频率
500600	0.10
600700	0.15
700800	0.40
800900	0.20
9001000	0.15
合计	1

 
（I）在下图中补齐频率分布直方图；
（II）估计元件寿命在500800h以内的概率。