高中数学误差估计试题

对某同学的6次数学测试成绩(满分100分)进行统计，作出的茎叶图如图所示，给出关于该同学数学成绩的以下说法：①中位数为84； ②众数为85；③平均数为85； ④极差为12.

其中，正确说法的序号是

A．①②

B．③④

C．②④

D．①③

甲、乙两个学习小组各有10名同学，他们在一次数学测验中成绩的茎叶图如下图所示，则他们在这次测验中成绩较好的是　　　　组。

某班的全体学生参加英语测试，成绩的频率分布直方图如图，数据的分组依次为：[20,40)，[40,60)，[60,80)，[80,100]．若低于60分的人数是15，则该班的学生人数是(   )

A．45	B．50
C．55	D．60

图1是某县参加2011年高考的学生身高条形统计图，从左到右的各条形图表示学生人数依次记为A1、A2、…A10（如A2表示身高（单位：cm）在[150，155内的人数]。图2是统计图1中身高在一定范围内学生人数的一个算法流程图。现要统计身高在160~180cm（含160cm，不含180cm）的学生人数，那么在流程图中的判断框内应填写的条件是（   ）

A．i<6

B．i<7

C．i<8

D．i<9

（本小题满分12分）某厂商调查甲、乙两种不同型号电视机在10个卖场的销售量（单位：台），并根据这10个卖场的销售情况，得到如图所示的茎叶图．
为了鼓励卖场，在同型号电视机的销售中，该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”．
（1）求在这10个卖场中，甲型号电视机的“星级卖场”的个数；
（2）若在这10个卖场中，乙型号电视机销售量的平均数为26．7，求的概率；
（3）若a=1，记乙型号电视机销售量的方差为，根据茎叶图推断b为何值时，达到最小值．（只需写出结论）

某电视台组织部分记者，用“10分制”随机调查某社区居民的幸福指数.现从调查人群中随机抽取16名，如图所示的茎叶图记录了他们的幸福指数的得分(以小数点前的一位数字为茎，小数点后的一位数字为叶)：

（1）指出这组数据的众数和中位数；
（2）若幸福指数不低于9.5分，则称该人的幸福指数为“极幸福”.求从这16人中随机选取3人，至多有1人是“极幸福”的概率；
（3）以这16人的样本数据来估计整个社区的总体数据，若从该社区(人数很多)任选3人，记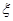表示抽到“极幸福”的人数，求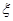的分布列及数学期望．

国家环境标准制定的空气质量指数与空气质量等级对应关系如下表：

由全国重点城市环境监测网获得2月份某五天甲城市和乙城市的空气质量指数数据用茎叶图表示如图：

（Ⅰ）试根据上面的统计数据，判断甲、乙两个城市的空气质量指数的方差的大小关系（只需写出结果）；
（Ⅱ）试根据上面的统计数据，估计甲城市某一天空气质量等级为2级良的概率；
（Ⅲ）分别从甲城市和乙城市的统计数据中任取一个，试求这两个城市空气质量等级相同的概率．
（注：s²=[（x₁﹣）²+（x₂﹣）²+…+（x_n﹣）²]，其中为数据x₁，x₂，…，x_n的平均数．）

2015年五一节”期间，高速公路车辆“较多，交警部门通过路面监控装置抽样调查某一山区路段汽车行驶速度，采用的方法是：按到达监控点先后顺序，每隔50辆抽取一辆，总共抽取120辆，分别记下其行车速度，将行车速度（km/h）分成七段[60，65），[65，70），[70，75），[75，80），[80，85），[85，90），[90，95）后得到如图所示的频率分布直方图，据图解答下列问题：

（1）求a的值，并说明交警部门采用的是什么抽样方法？
（2）若该路段的车速达到或超过90km/h即视为超速行驶，试根据样本估计该路段车辆超速行驶的概率；
（3）求这120辆车行驶速度的众数和中位数的估计值（精确到0．1）。

某校从高二年级学生中随机抽取60名学生，将其期中考试的政治成绩（均为整数）分成六段：，，…， 后得到如下频率分布直方图．

（Ⅰ）求分数在内的频率； 
（Ⅱ）根据频率分布直方图，估计该校高二年级学生期中考试政治成绩的平均分；
（Ⅲ）用分层抽样的方法在80分以上（含80分）的学生中抽取一个容量为6的样本，将该样本看成一个总体，从中任意选取2人，求其中恰有1人的分数．不低于90分的概率．

某校从参加高一年级期中考试的学生中随机抽出60名学生，将其数学成绩（均为整数）分成六段[40,50)，[50,60)，．．．，[90,100]后得到如图所示的部分频率分布直方图．观察图形的信息，回答下列问题：

（1）求分数在[70,80)内的频率，并补全这个频率分布直方图，统计方法中，同一组数据常用该组区间的中点值作为代表，据此估计本次考试的平均分；
（2）若从60名学生中随机抽取2人，抽到的学生成绩在[40,60)记0分，在[60,80)记1分，在[80,100]记2分，用表示抽取结束后的总记分，求的分布列和数学期望．

对某班学生是爱好体育还是爱好文娱进行调查，根据调查得到的数据，所绘制的二维条形图如图．
（1）根据图中的数据，填好2×2列表，并计算在多大的程度上可以认为性别与是否爱好体育有关系：
（2）若已从男生中选出3人，女生中选出2人，从这5人中选出2人担任活动的协调人，求选出的两人性别相同的概率．

	男	女	总计
爱好体育
爱好文娱
总  计

参考数据：

	0．5	0．4	0．25	0．15	0．10	0．05	0．025	0．010	0．005	0．001
	0．455	0．708	1．323	2．072	2．706	3．841	5．024	6．635	7．879	10．828

参考公式：

《中华人民共和国道路交通安全法》规定：车辆驾驶员血液酒精浓度在20～80mg/100ml（不含80）之间，属于酒后驾车；在80mg/100ml（含80）以上时，属于醉酒驾车．某市公安局交通管理部门在某路段的一次拦查行动中，依法检查了300辆机动车，查处酒后驾车和醉酒驾车的驾驶员共20人，检测结果如下表：

（1）绘制出检测数据的频率分布直方图（在图中用实线画出矩形框即可）；
（2）求检测数据中醉酒驾驶的频率，并估计检测数据中酒精含量的众数、平均数．

将容量为n的样本中的数据分成6组，绘制频率分布直方图. 若第一组至第六组数据的频率之比为2:3:4:6: 4:1，且前三组数据的频数之和等于36，则n等于   ．

某高校在2011年的自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组：第1组[75，80)，第2组[80，85)，第3组[85，90)，第4组[90，95)，第5组
[95，100]得到的频率分布直方图如图所示．
(1)分别求第3，4，5组的频率；
(2)若该校决定在笔试成绩高的第3，4，5组中用分层抽样抽取6名学生进入第二轮面试，求第3，4，5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下，学校决定在这6名学生中随机抽取2名学生接受甲考官的面试，求第4组至少有一名学生被甲考官面试的概率．

某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50,60)，[60,70)，[70,80)，[80,90)，[90,100].

（1）求图中a的值；
（2）根据频率分布直方图，估计这100名学生语文成绩的平均分；
（3）若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示，求数学成绩在[50,90)之外的人数.

分数段	[50,60)	[60,70)	[70,80)	[80,90)
x∶y	1∶1	2∶1	3∶4	4∶5