2013届新课标高三配套第四次月考文科数学试卷
已知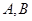 是非空集合,命题甲:
是非空集合,命题甲: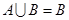 ,命题乙:
,命题乙: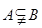 ,那么( )
,那么( )
| A.甲是乙的充分不必要条件 | B.甲是乙的必要不充分条件 |
| C.甲是乙的充要条件 | D.甲是乙的既不充分也不必要条件 |
一个总体分为A,B,C三层,用分层抽样方法从总体中抽取一个容量为50的样本,
已知B层中每个个体被抽到的概率都为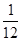 ,则总体中的个数为( )
,则总体中的个数为( )
| A.150 | B.200 | C.500 | D.600 |
现有2名女教师和1名男教师参加说题比赛,共有2道备选题目,若每位选手从
中有放回地随机选出一道题进行说题,其中恰有一男一女抽到同一道题的概率为( )
A.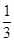 |
B.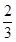 |
C.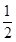 |
D.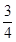 |
为了了解某校高三400名学生的数学学业水平测试成绩,制成样本频率分布直方图如图1,规定不低于60分为及格,不低于80分为优秀,则及格率与优秀人数分别是( )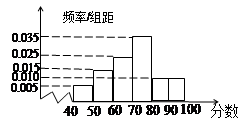
| A.60%,60 | B.60%,80 | C.80%,80 | D.80%,60 |
设不等式组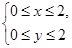 表示的平面区域为D,在区域D内随机取一个点,则此点到坐标原点的距离大于2的概率是( )
表示的平面区域为D,在区域D内随机取一个点,则此点到坐标原点的距离大于2的概率是( )
A. |
B.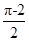 |
C.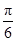 |
D.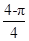 |
定义在R上的函数f(x)满足f(x+6)=f(x).当-3≤x<-1时,f(x)=-(x+2)2;
当-1≤x<3时,f(x)=x,则f(1)+f(2)+f(3)+…+f(2 012)=( )
| A.335 | B.338 | C.1 678 | D.2 012 |
已知四棱锥P-ABCD的侧棱长与底面边长都相等,点 是
是 的中点,则异面直
的中点,则异面直
线 与
与 所成角的余弦值为( )
所成角的余弦值为( )
A. |
B. |
C. |
D. |
小华的妈妈经营一家饮品店,经常为进货数量而烦恼,于是小华
代妈妈进行统计,其中某种饮料的日销售量y(瓶)与当天的气温x(℃)的几组对照数据
如下:
| x |
10 |
15 |
20 |
25 |
30 |
| y |
110 |
125 |
160 |
185 |
220 |
根据上表得回归方程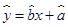 中的
中的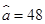 ,据此模型估计当气温为35℃时,该饮料的日销售量为 瓶.
,据此模型估计当气温为35℃时,该饮料的日销售量为 瓶.
为了解本市居民的生活成本,甲、乙、丙三名同学利用假期分别对三个社区进行
了“家庭每月日常消费额”的调查.他们将调查所得到的数据分别绘制成频率分布直方图
(如图所示),记甲、乙、丙所调查数据的标准差分别为s1、s2、s3,则它们的大小关系
为 .(用“>”连接)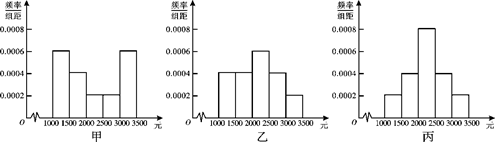
已知函数 (其中
(其中 ,
, ,
, )的部分图象如图所示.
)的部分图象如图所示.
(1)求 ,
, ,
, 的值;
的值;
(2)已知在函数 图象上的三点
图象上的三点 的横坐标分别为
的横坐标分别为 ,求
,求 的值.
的值.
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示,求数学成绩在[50,90)之外的人数.
| 分数段 |
[50,60) |
[60,70) |
[70,80) |
[80,90) |
| x∶y |
1∶1 |
2∶1 |
3∶4 |
4∶5 |
如图,直三棱柱ABC-A′B′C′,∠BAC=90°,AB=AC= ,AA′=1,点M,N分别为A′B和B′C′的中点.
,AA′=1,点M,N分别为A′B和B′C′的中点.
(1)证明:MN∥平面A′ACC′;
(2)求三棱锥A′-MNC的体积.
(锥体体积公式V= Sh,其中S为底面面积,h为高)
Sh,其中S为底面面积,h为高)
如图6所示,等边三角形OAB的边长为8 ,且其三个顶点均在抛物线E:x2=2py(p>0)上.
,且其三个顶点均在抛物线E:x2=2py(p>0)上.
图6
(1)求抛物线E的方程;
(2)设动直线l与抛物线E相切于点P,与直线y=-1相交于点Q,证明以PQ为直径的圆恒过y轴上某定点.
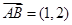 ,
,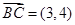 ,则
,则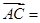 ( )
( )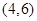
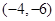
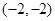
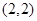
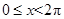 ,且
,且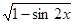 =
=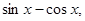 则( )
则( )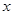 ≤
≤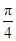 ≤
≤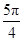
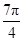
 ≤
≤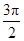
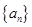 中,
中,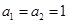 ,且
,且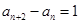 ,则数列
,则数列 的左、右焦点分别为
的左、右焦点分别为 为
为 的右支上一点,且
的右支上一点,且 ,则
,则 等于( )
等于( ) 在点
在点 处的切线为l,则l上的点到
处的切线为l,则l上的点到 上的
上的



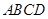 内部随机取一点
内部随机取一点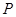 ,则
,则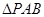 的面积大于等于
的面积大于等于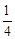 的
的 对任意
对任意 ,满足
,满足 .
. ,求
,求 的通项公式及前
的通项公式及前 项和.
项和. x3+
x3+ x2-ax-a,x∈R,其中a>0.
x2-ax-a,x∈R,其中a>0. 粤公网安备 44130202000953号
粤公网安备 44130202000953号