已知 是三条不同的直线,
是三条不同的直线,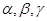 是三个不同的平面,下列命题:
是三个不同的平面,下列命题:
①若 ,
, ,则
,则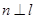 ; ②若
; ②若 ,
,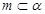 ,则
,则 ;
;
③若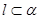 ,
, ,
, ,则
,则 ; ④若
; ④若 ,则
,则 .
.
其中真命题是_ __.(写出所有真命题的序号).
如图 所在平面,
所在平面, 是
是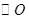 的直径,
的直径, 是
是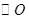 上一点,
上一点, ,
, ,给出下列结论:①
,给出下列结论:①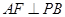 ; ②
; ②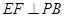 ;③
;③ ; ④平面
; ④平面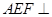 平面
平面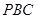 ⑤
⑤ 是直角三角形
是直角三角形
其中正确的命题的序号是 
如图, 是
是 的直径,
的直径, 垂直于
垂直于 所在的平面,
所在的平面, 是圆周上不同于
是圆周上不同于 的任意一点,则图中直角三角形有 个.(要求:只需填直角三角形的个数,不需要具体指出三角形名称).
的任意一点,则图中直角三角形有 个.(要求:只需填直角三角形的个数,不需要具体指出三角形名称).
给定下列四个命题:
①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
③垂直于同一直线的两条直线相互平行;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.其中,为真命题的是 。
设m,n是两条不同的直线, ,
, ,
, 是三个不同的平面,给出下列命题:
是三个不同的平面,给出下列命题:
①若 ,
, ,则
,则 ;
;
②若 ,
, ,则
,则 ;
;
③若 ,
, ,则
,则 ;
;
④若 ,
, ,
, ,则
,则 .
.
上面命题中,真命题的序号是 (写出所有真命题的序号).
在棱长为1的正方体ABCD﹣A1B1C1D1中,过对角线BD1的一个平面交AA1于E,交CC1于F,得四边形BFD1E,给出下列结论:
①四边形BFD1E有可能为梯形
②四边形BFD1E有可能为菱形
③四边形BFD1E在底面ABCD内的投影一定是正方形
④四边形BFD1E有可能垂直于平面BB1D1D
⑤四边形BFD1E面积的最小值为
其中正确的是 (请写出所有正确结论的序号)
已知是两条不同的直线,是两个不同的平面,有下列五个命题
① ②
②
③ ④
④
⑤
其中真命题的序号是__________________________(把所有真命题的序号都填上)
点P在正方体 的面对角线
的面对角线 上运动,则下列四个命题:
上运动,则下列四个命题: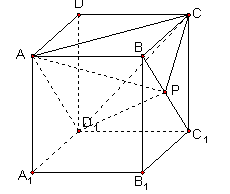
①三棱锥 的体积不变;
的体积不变;
②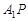 ∥平面
∥平面 ;
;
③ ;
;
④平面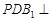 平面
平面 .
.
其中正确的命题序号是 .
设 和
和 为不重合的两个平面,给出下列命题:
为不重合的两个平面,给出下列命题:
(1)若 内的两条相交直线分别平行于
内的两条相交直线分别平行于 内的两条直线,则
内的两条直线,则 平行于
平行于 ;
;
(2)若 外一条直线
外一条直线 与
与 内的一条直线平行,则
内的一条直线平行,则 和
和 平行;
平行;
(3)设 和
和 相交于直线
相交于直线 ,若
,若 内有一条直线垂直于
内有一条直线垂直于 ,则
,则 和
和 垂直;
垂直;
(4)直线 与
与 垂直的充分必要条件是
垂直的充分必要条件是 与
与 内的两条直线垂直.
内的两条直线垂直.
上面命题中,真命题的序号 (写出所有真命题的序号).