三棱锥 中,
中, 若
若 ,
, 是该三棱锥外部(不含表面)的一点,给出下列四个命题,
是该三棱锥外部(不含表面)的一点,给出下列四个命题,
① 存在无数个点 ,使
,使 ;
;
② 存在唯一点 ,使四面体
,使四面体 为正三棱锥;
为正三棱锥;
③ 存在无数个点 ,使
,使 ;
;
④ 存在唯一点 ,使四面体
,使四面体 有三个面为直角三角形.
有三个面为直角三角形.
其中正确命题的序号是 .
如图,四边形
为菱形,
=120°,
是平面
同一侧的两点,
⊥平面
,
⊥平面
,
,
.
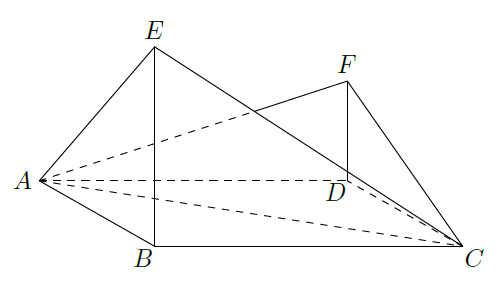
(Ⅰ)证明:平面
⊥平面
;
(Ⅱ)求直线
与直线
所成角的余弦值.
一个正方体的平面展开图及该正方体的直观图的示意图如图所示:
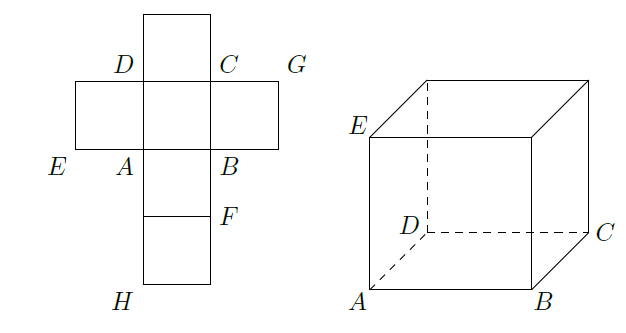
(Ⅰ)请按字母
标记在正方体相应地顶点处(不需要说明理由)
(Ⅱ)判断平面
与平面
的位置关系,并说明你的结论.
(Ⅲ)证明:直线
平面
.
四棱锥P﹣ABCD中,底面ABCD是边长为8的菱形,∠BAD= ,若PA=PD=5,平面PAD⊥平面ABCD.
,若PA=PD=5,平面PAD⊥平面ABCD.
(1)求四棱锥P﹣ABCD的体积;
(2)求证:AD⊥PB.
如图,直三棱柱ABC﹣A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
(Ⅰ)求证:MN∥平面ABB1A1;
(Ⅱ)线段CC1上是否存在点Q,使A1B⊥平面MNQ?说明理由.
如图(1),在三角形ABC中,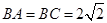 ,
,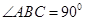 ,点O、M、N分别为线段的中点,将ABO和MNC分别沿BO,MN折起,使平面ABO与平面CMN都与底面OMNB垂直,如图(2)所示.
,点O、M、N分别为线段的中点,将ABO和MNC分别沿BO,MN折起,使平面ABO与平面CMN都与底面OMNB垂直,如图(2)所示.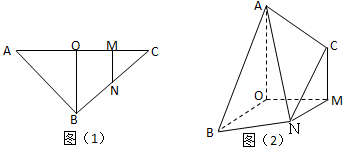
(1)求证: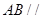 平面CMN;
平面CMN;
(2)求点M到平面CAN的距离.
如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到A1点,且A1在平面BCD上的射影O恰好在CD上.
(1)求证:BC⊥A1D.
(2)求证:平面A1BC⊥平面A1BD.
(3)求三棱锥A1-BCD的体积.