在三棱柱ABC-A1B1C1中,△ABC与△A1B1C1都为正三角形且AA1⊥面ABC,F、F1分别是AC,A1C1的中点。
求证:(1)平面AB1F1∥平面C1BF;
(2)平面AB1F1⊥平面ACC1A1.
(本小题满分12分)如图,在底面是正方形的四棱锥P—ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
(1)求证:BD⊥FG;
(2)当二面角B—PC—D的大小为 时,求PC与底面ABCD所成角的正切值.
时,求PC与底面ABCD所成角的正切值.
已知棱长为l的正方体 中,E,F,M分别是AB、AD、
中,E,F,M分别是AB、AD、 的中点,又P、Q分别在线段
的中点,又P、Q分别在线段 上,且
上,且 设面
设面 面MPQ=
面MPQ= ,则下列结论中不成立的是( )
,则下列结论中不成立的是( )
A. 面ABCD
面ABCD
B. AC
AC
C.面MEF与面MPQ不垂直
D.当x变化时, 不是定直线
不是定直线
(本小题满分12分)如图所示,在四棱锥 中,底面ABCD为菱形,
中,底面ABCD为菱形, ,Q为AD的中点.
,Q为AD的中点.
(Ⅰ)若 ,求证:平面
,求证:平面 平面
平面 ;
;
(Ⅱ)点M在线段PC上,二面角 为
为 ,若平面
,若平面
 平面ABCD,且
平面ABCD,且 ,
,
求三棱锥 的体积.
的体积.
如图,在正三棱柱ABC-A1B1C1中,A1A=AC,D,E,F分别为线段AC,A1A,C1B的中点.

(1)证明:EF∥平面ABC;
(2)证明:C1E⊥平面BDE.
(本小题满分12分)如图,已知 是圆
是圆 的直径,
的直径, ,
, 是⊙
是⊙ 上一点,且
上一点,且 ,
, ,
, ,
,
 是
是 的中点,
的中点, 是
是 的中点
的中点

(1)求证: 平面
平面 ;
;
(2)求证: 平面
平面 ;
;
(3)求 与平面
与平面 所成角的大小
所成角的大小
如图,正方体ABCD—A1B1C1D1中,O为底面ABCD的中心,
M为棱BB1的中点,则下列结论中错误的是( )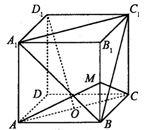
| A.D1O∥平面A1BC1 |
| B.D1O⊥平面AMC |
| C.异面直线BC1与AC所成的角等于60° |
| D.二面角M-AC-B等于45° |