广东省肇庆市高中毕业班第一次统一检测理科数学试卷
已知全集U={1,2,3,4,5,6},集合M={1,3,5},则
A. |
B.{1,3,5} | C.{2,4,6} | D.{1,2,3,4,5,6} |
设条件p: ;条件q:
;条件q: ,那么p是q的
,那么p是q的
| A.充分条件 | B.必要条件 | C.充要条件 | D.非充分非必要条件 |
设 是非零向量,已知命题p:若
是非零向量,已知命题p:若 ,
, ,则
,则 ;命题q:若
;命题q:若 ,
, ,则
,则 . 则下列命题中真命题是
. 则下列命题中真命题是
A. |
B. |
C. |
D. |
一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该几何体的外接球的表面积为
A. |
B. |
C. |
D. |
现有16张不同的卡片,其中红色、黄色、蓝色、绿色卡片各4张,从中任取3张,要求这三张卡片不能是同一种颜色,且绿色卡片至多1张,不同的取法的种数为
| A.484 | B.472 | C.252 | D.232 |
设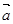 ,
, 为非零向量,
为非零向量,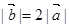 ,两组向量
,两组向量 和
和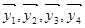 均由2个
均由2个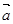 和2个
和2个 排列而成. 若
排列而成. 若 所有可能取值中的最小值为
所有可能取值中的最小值为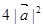 ,则
,则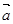 与
与 的夹角为
的夹角为
A.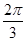 |
B.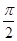 |
C.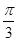 |
D.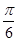 |
(几何证明选讲)如图,点P为圆O的弦AB上的一点,连接PO,过点P作PC^OP,且PC交圆O于C. 若AP=4,PC=2,则PB= .
(本小题满分12分)为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间x(单位:小时)与当天投篮命中率y之间的关系:
| 时间x |
1 |
2 |
3 |
4 |
5 |
| 命中率y |
0.4 |
0.5 |
0.6 |
0.6 |
0.4 |
(1)求小李这5天的平均投篮命中率;
(2)用线性回归分析的方法,预测小李该月6号打6小时篮球的投篮命中率.
(本小题满分12分)如图,已知 是圆
是圆 的直径,
的直径, ,
, 是⊙
是⊙ 上一点,且
上一点,且 ,
, ,
, ,
,
 是
是 的中点,
的中点, 是
是 的中点
的中点

(1)求证: 平面
平面 ;
;
(2)求证: 平面
平面 ;
;
(3)求 与平面
与平面 所成角的大小
所成角的大小
(本小题满分14分)某商店根据以往某种玩具的销售记录,绘制了日销售量的频率分布直方图,如图所示,将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立
(1)估计日销售量的众数;
(2)求在未来连续3天里,有连续2天的日销售量都不低于100个且另一天的日销售量低于50个的概率;
(3)用 表示在未来3天里日销售量不低于100个的天数,求随机变量
表示在未来3天里日销售量不低于100个的天数,求随机变量 的分布列,期望
的分布列,期望 及方差
及方差 .
.
(本小题满分14分)
某家电生产企业根据市场调查分析,决定调整新产品生产方案,准备每周(按40个工时计算)生产空调器、彩电、冰箱共120台,且冰箱至少生产20台. 已知生产这些家电产品每台所需工时和每台产值如下表:
| 家电名称 |
空调器 |
彩电 |
冰箱 |
| 工 时 |
 |
 |
 |
| 产值/千元 |
4 |
3 |
2 |
问每周应生产空调器、彩电、冰箱各多少台,才能使产值最高?最高产值是多少?(以千元为单位)
(本小题满分14分)如图,四棱柱 中,
中, ^底面ABCD,且
^底面ABCD,且 . 梯形ABCD的面积为6,且AD//BC,AD=2BC,
. 梯形ABCD的面积为6,且AD//BC,AD=2BC, . 平面
. 平面 与
与 交于点E.
交于点E. 
(1)证明:EC// ;
;
(2)求三棱锥 的体积;
的体积;
(3)求二面角 的大小.
的大小.






 ,
, ,若
,若 ,则
,则 .
. 是纯虚数,则实数a的值为 .
是纯虚数,则实数a的值为 . 的展开式中
的展开式中 的系数为
的系数为 .
. 解集为
解集为 .
. ,
, ,且
,且 ,则
,则 的最小值为 .
的最小值为 . .
. ;
; .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号