（本小题满分14分）
某家电生产企业根据市场调查分析，决定调整新产品生产方案，准备每周（按40个工时计算）生产空调器、彩电、冰箱共120台，且冰箱至少生产20台. 已知生产这些家电产品每台所需工时和每台产值如下表：
| 家电名称 |
空调器 |
彩电 |
冰箱 |
| 工 时 |
 |
 |
 |
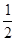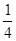| 产值/千元 |
4 |
3 |
2 |
问每周应生产空调器、彩电、冰箱各多少台，才能使产值最高？最高产值是多少？（以千元为单位）
推荐套卷
（本小题满分14分）
某家电生产企业根据市场调查分析，决定调整新产品生产方案，准备每周（按40个工时计算）生产空调器、彩电、冰箱共120台，且冰箱至少生产20台. 已知生产这些家电产品每台所需工时和每台产值如下表：
| 家电名称 |
空调器 |
彩电 |
冰箱 |
| 工 时 |
|
|
|
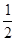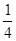| 产值/千元 |
4 |
3 |
2 |
问每周应生产空调器、彩电、冰箱各多少台，才能使产值最高？最高产值是多少？（以千元为单位）
粤公网安备 44130202000953号