在三棱柱ABC－A1B1C1中，△ABC与△A1B1C1都为正三角形且AA1⊥面ABC，F、F1分别是AC，A1C1的中点。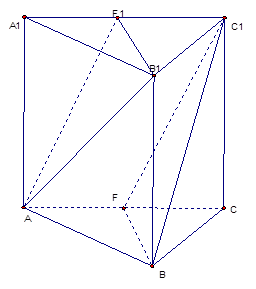
求证：（1）平面AB1F1∥平面C1BF；
（2）平面AB1F1⊥平面ACC1A1.
，求这个三角形的顶角的正弦、余弦及正切值．
中，
，
，求
的值．
，
，求证：
．
，求证
．
，
，求
的值．推荐套卷
在三棱柱ABC－A1B1C1中，△ABC与△A1B1C1都为正三角形且AA1⊥面ABC，F、F1分别是AC，A1C1的中点。
求证：（1）平面AB1F1∥平面C1BF；
（2）平面AB1F1⊥平面ACC1A1.
粤公网安备 44130202000953号