如图,空间四边形SABC中,SO⊥平面ABC,O为△ABC的垂心。求证:平面SOC ⊥平面SA B。
B。
如图,四棱锥S-ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,SB=
(1)求证:BC⊥SC; (2)设棱SA的中点为M,求证:DM⊥SB.
已知正方体ABCD-A1B1C1D1的棱长为a. (1)求证:平面ACD1∥平面BA1C1;
(2)求证:平面BDD1B1⊥平面BA1C1。
|
|
|
|

有下列四个命题,其中正确的命题有( )
①A、B到a的距离相等,则AB∥a;②?ABC的三个顶点到平面a的距离相等,则平面ABC∥a;③夹在两个平行平面间的平行线段相等;④垂直于同一个平面的两条直线互相平行.
A ①② B ②③ C ③ D ③④
两条异面直线在同一平面内的射影是( )
A 两条相交直线 B 两条平行直线
C 一条直线和不在这条直线上的一个点 D 以上位置均有可能。
如图,设平面 垂足分别是B、D,如果增加一个条件,就能推出
垂足分别是B、D,如果增加一个条件,就能推出 EF,这个条件不可能是下面四个选项中的( )
EF,这个条件不可能是下面四个选项中的( )
A. 
B. 
C. AC与BD在b内的射影在同一条直线上
D.  与a、b所成的角相等
与a、b所成的角相等
已知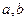 为直线,
为直线,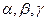 为平面,有下列三个命题:
为平面,有下列三个命题:
(1)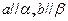 ,则
,则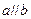 ;
;
(2)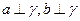 ,则
,则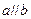 ;
;
(3)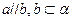 ,则
,则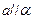 ;
;
(4)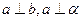 ,则
,则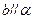 ;
;
其中正确命题是