在阳光下将一个球放在水平面上,球的影子伸到距球与地面接触点 处,同一时刻,一个长
处,同一时刻,一个长 ,一端接触地面且与地面垂直的竹竿的影子长为
,一端接触地面且与地面垂直的竹竿的影子长为 ,则该球的半径等于( )
,则该球的半径等于( )
A. |
B. |
C. |
D. |
如图,四棱锥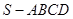 的底面为正方形,
的底面为正方形, 底面
底面 ,则下列结论中不正确的是
,则下列结论中不正确的是
A.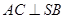 |
B. 平面 平面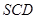 |
C. 与平面 与平面 所成的角等于 所成的角等于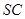 与平面  所成的角; 所成的角; |
D. 与 与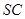 所成的角等于 所成的角等于 与 与 所成的角。 所成的角。 |

下面命题中错误的是
A.如果平面 平面 平面 ,那么平面 ,那么平面 内一定存在直线平行于平面 内一定存在直线平行于平面 ; ; |
B.如果平面 不垂直于平面 不垂直于平面 ,那么平面 ,那么平面 内一定不存在直线垂直于平面 内一定不存在直线垂直于平面 ; ; |
C.如果平面 平面 平面 ,平面 ,平面 平面 平面 , , ,那么 ,那么 平面 平面 ; ; |
D.如果平面 平面 平面 ,那么平面 ,那么平面 内所有直线都垂直于平面 内所有直线都垂直于平面 。 。 |
在空间,以下命题中真命题的个数为
①垂直同一条直线的两条直线平行;
②到定点距离等于定长的点的轨迹是圆;
③有三个角是直角的四边形是矩形;
④自一点向一条已知直线引垂线有且只有一条。
| A.0 | B.1 | C.2 | D.3 |
如图,在四棱锥 中, 平面 , =4, =3, =5, = =90°, 是 的中点.

(Ⅰ)证明:
平面
;
(Ⅱ)若直线
与平面
所成的角和
与平面
所成的角相等,求四棱锥
的体积.
在空间给出下面四个命题(其中 、
、 为不同的两条直线),
为不同的两条直线), 、
、 为不同的两个平面)
为不同的两个平面)
①

②
③
④
其中正确的命题个数有
| A.1个 | B.2个 | C.3个 | D.4个 |
如图,四棱锥S—ABCD的底面为正方形,SD 底面ABCD,
底面ABCD,
则下列结论中不正确的是
| A.AC⊥SB |
| B.AB∥平面SCD |
| C.SA与平面SBD所成的角等于SC与平面SBD所成的角 |
| D.AB与SC所成的角等于DC与SA所成的角 |

如图,在正三棱柱ABC-A1B1C1中,底面ABC为正三角形,M、N、G分别是棱CC1、AB、BC的中点,且 .
.
(Ⅰ)求证:CN∥平面AMB1;
(Ⅱ)求证: B1M⊥平面AMG.
如图,在三棱锥 中,三条棱
中,三条棱 ,
, ,
, 两两垂直,且
两两垂直,且 >
> >
> ,分别经过三条棱
,分别经过三条棱 ,
, ,
, 作一个截面平分三棱锥的体积,截面面积依次为
作一个截面平分三棱锥的体积,截面面积依次为 ,
, ,
, ,则
,则 ,
, ,
, 的大小关系为 。
的大小关系为 。
在棱长为1的正方体ABCD—A1B1C1D1中,点P是它的体对角线BD1上一动点,则|AP|+|PC|的最小值是_________
一个正方体的展开图如图示,C、D为原正方体的顶点,AB为原正方体的棱的中点,在原正方体中,CD与AB所成角的余弦值为( )
A、0 B、 C、
C、 D、
D、

E、F分别是边长为2的正方形ABCD的边BC、CD的中点,沿AE、EF和FA分别将△ABE、△ECF和△AFD折起,使B、C、D重合为一点G得到一个三棱锥G—AEF,则它的体积为( )
A、 B、
B、 C、
C、 D、1
D、1
(p) 如图,ABCD-A1B1C1D1为正方体,下面结论错误的是
| A.BD//平面CB1D1 |
| B.AC1⊥BD |
| C.AC1⊥平面CB1D1 |
| D.异面直线AD与CB1所成的角为60° |