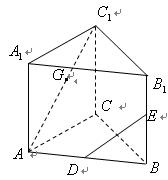
(本小题满分12分)如图,在正三棱柱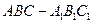 中,
中,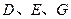 分别是
分别是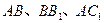 的中点,
的中点,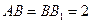 .
.
(Ⅰ)在棱 上是否存在点
上是否存在点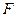 使
使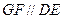 ?如果存在,试确定它的位置;如果不存在,请说明理由;
?如果存在,试确定它的位置;如果不存在,请说明理由;
(Ⅱ)求截面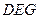 与底面
与底面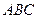 所成锐二面角的正切值;
所成锐二面角的正切值;
(Ⅲ)求点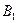 到截面
到截面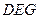 的距离.
的距离.
(本小题满分12分)
如图6,已知正三棱柱ABC—A1B1C1中,D是BC的中点,AA1=AB=1。
(1)求证:平面AB1D⊥平面B1BCC1;
(2)求证:A1C//平面AB1D;
(3)求二面角B—AB1—D的正切值。
(本小题共13分)
如图,在四棱锥P—ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠ABC=
∠BAD=90°, 为AB中点,F为PC中点.
为AB中点,F为PC中点.
(I)求证:PE⊥BC;
(II)求二面角C—PE—A的余弦值;
(III)若四棱锥P—ABCD的体积为4,求AF的长.
(本小题满分12分)
在四棱锥 中,底面
中,底面 是一直角梯形,
是一直角梯形, ,
, ,
, 底面
底面 .
.
(1)求三棱锥 的体积;
的体积;
(2)在 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 ,若存在,求出
,若存在,求出 的值;若不存在,试说明理由.
的值;若不存在,试说明理由.