调查了某地若干户家庭的年收x(单位:万元)和年饮食支出y(单位:万元),调查显示年收入x与年饮食支出y具有线性相关关系,井由调查数据得到y对x的回归直线方程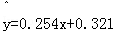 .由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加 万元.
.由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加 万元.
具有线性相关关系的变量x,y,满足一组数据如下表所示:

若y与x的回归直线方程为 ,则m的值是 .
,则m的值是 .
某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如右数据:
单价 (元) (元) |
8 |
8.2 |
8.4 |
8.6 |
8.8 |
9 |
销量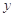 (件) (件) |
90 |
84 |
83 |
80 |
75 |
68 |
由表中数据,求得线性回归方程为 .若在这些样本点中任取一点,则它在回归直线左下方的概率为_______.
.若在这些样本点中任取一点,则它在回归直线左下方的概率为_______.
在一组样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2,…,xn不全相等)的散点图中,若所有样本点(xi,yi)(i=1,2,…,n)都在直线y= x+1上,则这组样本数据的样本相关系数为 .
x+1上,则这组样本数据的样本相关系数为 .
已知x、y的取值如下表所示,若y与x线性相关,且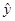 =0.95x+
=0.95x+ ,则
,则 =____________.
=____________.
| x |
0 |
1 |
3 |
4 |
| y |
2.2 |
4.3 |
4.8 |
6.7 |
已知具有线性相关关系的变量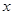 和
和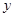 ,测得一组数据如下表:若已求得它们的回归直线方程的斜率为6.5,则这条回归直线的方程为 .
,测得一组数据如下表:若已求得它们的回归直线方程的斜率为6.5,则这条回归直线的方程为 .
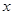 |
2 |
4 |
5 |
6 |
8 |
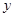 |
10 |
20 |
40 |
30 |
50 |
若下表数据对应的 关于
关于 的线性回归方程为
的线性回归方程为 ,则
,则 = .
= .
 |
3 |
4 |
5 |
6 |
 |
2.5 |
3 |
4 |
4.5 |
某地区恩格尔系数(表示生活水平高低的一个指标)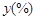 与年份
与年份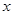 的统计数据如下表:
的统计数据如下表:
年份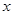 |
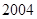 |
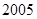 |
 |
 |
恩格尔系数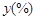 |
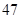 |
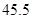 |
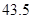 |
 |
从散点图可以看出 与
与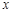 线性相关,且可得回归直线方程为
线性相关,且可得回归直线方程为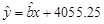 ,据此模型可预测
,据此模型可预测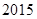 年该地区的恩格尔系数为
年该地区的恩格尔系数为  .
.
某地区恩格尔系数(表示生活水平高低的一个指标)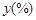 与年份
与年份 的统计数据如下表:
的统计数据如下表:
年份 |
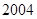 |
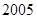 |
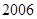 |
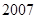 |
恩格尔系数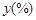 |
 |
 |
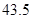 |
 |
从散点图可以看出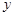 与
与 线性相关,且可得回归直线方程为
线性相关,且可得回归直线方程为 ,据此模型可预测
,据此模型可预测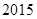 年该地区的恩格尔系数为
年该地区的恩格尔系数为  .
.
一物体沿直线以速度 (
(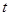 的单位为:秒,
的单位为:秒,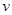 的单位为:米/秒)的速度作变速直线运动,则该物体从时刻t=0秒至时刻 t=5秒间运动的路程是_______
的单位为:米/秒)的速度作变速直线运动,则该物体从时刻t=0秒至时刻 t=5秒间运动的路程是_______
某食品的保鲜时间 (单位:小时)与储存温度 (单位: )满足函数关系 ( 为自然对数的底数, 为常数).若该食品在 的保鲜时间设计192小时,在 的保鲜时间是48小时,则该食品在的 保鲜时间是小时.