辽宁省五校协作体高三上学期期初考试理科数学试卷
设集合 则
则 =( )
=( )
| A.{0,1,2,3,} | B.{5} | C.{1,2,4} | D.{0,4,5} |
给出下列四个命题, 其中错误的命题有( )个.
(1)函数 上的单调递增区间是
上的单调递增区间是 ;
;
(2)设随机变量  ,若
,若 ,则
,则 ;
;
(3)设函数 ,
, 的图象向左平移
的图象向左平移 个单位,得到一个偶函数的图象;
个单位,得到一个偶函数的图象;
(4)“直线 与直线
与直线 互相垂直”的充分条件是“
互相垂直”的充分条件是“ ”
”
| A.0 | B.1 | C.2 | D.3 |
曲线 在点(1,2)处的切线为
在点(1,2)处的切线为 ,则直线
,则直线 上的任意点P与圆
上的任意点P与圆 上的任意点Q之间的最近距离是( )
上的任意点Q之间的最近距离是( )
A. |
B. |
C. |
D.2 |
几何体的三视图如图所示,若从该几何体的实心外接球中挖去该几何体,则剩余几何体的表面积是(注:包括外表面积和内表面积)( )

A.133 |
B.100 |
C.66 |
D.166 |
已知 分别为双曲线
分别为双曲线 的左、右焦点,P为双曲线右支上的任意一点,若
的左、右焦点,P为双曲线右支上的任意一点,若 的最小值为8
的最小值为8 ,则双曲线的离心率
,则双曲线的离心率 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如右数据:
单价 (元) (元) |
8 |
8.2 |
8.4 |
8.6 |
8.8 |
9 |
销量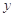 (件) (件) |
90 |
84 |
83 |
80 |
75 |
68 |
由表中数据,求得线性回归方程为 .若在这些样本点中任取一点,则它在回归直线左下方的概率为_______.
.若在这些样本点中任取一点,则它在回归直线左下方的概率为_______.
已知抛物线C: 的焦点为F,过点F倾斜角为
的焦点为F,过点F倾斜角为 的直线
的直线 与抛物线C在第一、四象限分别交于A、B两点,则
与抛物线C在第一、四象限分别交于A、B两点,则 的值等于 .
的值等于 .

某大学志愿者协会中,数学学院志愿者有8人,其中含5名男生,3名女生;外语学院志愿者有4人,其中含1名男生,3名女生.现采用分层抽样的方法(层内采用简单随机抽样)从两个学院中共抽取3名同学,到希望小学进行支教活动.
(1)求从数学学院抽取的同学中至少有1名女同学的概率;
(2)记 为抽取的
为抽取的 名同学中男同学的人数,求随机变量
名同学中男同学的人数,求随机变量 的分布列和数学期望.
的分布列和数学期望.
如图,在三棱锥 底面ABC,且SB=
底面ABC,且SB= 分别是SA、SC的中点.
分别是SA、SC的中点.
(Ⅰ)求证:平面 平面BCD;
平面BCD;
(Ⅱ)求二面角 的平面角的大小.
的平面角的大小.
(本小题满分12分)已知椭圆 +
+ =1(
=1( >
> >
> )的离心率为
)的离心率为 ,且过点(
,且过点( ,
, ).
).
(1)求椭圆方程;
(2)设不过原点 的直线
的直线 :
:
 ,与该椭圆交于
,与该椭圆交于 、
、 两点,直线
两点,直线 、
、 的斜率依次为
的斜率依次为 、
、 ,满足
,满足 ,试问:当
,试问:当 变化时,
变化时, 是否为定值?若是,求出此定值,并证明你的结论;若不是,请说明理由.
是否为定值?若是,求出此定值,并证明你的结论;若不是,请说明理由.
(本小题满分12分)已知函数 (
( 为自然对数的底数).
为自然对数的底数).
(1)求函数 的单调区间;
的单调区间;
(2)设函数 ,存在
,存在 使得
使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(本小题满分10分)选修4-1:几何证明选讲
如图, 是的⊙
是的⊙ 直径,
直径, 与⊙
与⊙ 相切于
相切于 ,
, 为线段
为线段 上一点,连接
上一点,连接 、
、 , 分别交⊙
, 分别交⊙ 于
于 、
、 两点,连接
两点,连接 交
交 于点
于点 .
.
(Ⅰ)求证: 、
、 、
、 、
、 四点共圆.
四点共圆.
(Ⅱ)若 为
为 的三等分点且靠近
的三等分点且靠近 ,
, ,
, ,求线段
,求线段 的长.
的长.
(本小题满分10分)选修4-4:坐标系与参数方程
已知在直角坐标系 中,直线
中,直线 的参数方程为
的参数方程为 ,(
,( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为
(Ⅰ)求直线 的普通方程和曲线
的普通方程和曲线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设点 是曲线
是曲线 上的一个动点,求它到直线
上的一个动点,求它到直线 的距离
的距离 的取值范围.
的取值范围.
 满足
满足 为虚数单位),则
为虚数单位),则 ( )
( )



 的公比
的公比 ,且
,且 成等差数列,则
成等差数列,则 的值为( )
的值为( )


 ,
, ,则输出
,则输出 的值分别是( )
的值分别是( )




 与
与 的夹角为60°,
的夹角为60°, 则
则 ( )
( )

 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时,
时, 则
则 ,直线
,直线 及
及 轴所围成的曲边四边形的面积为( )
轴所围成的曲边四边形的面积为( )



 ,不等式
,不等式 恒成立,则下列不等式错误的是
恒成立,则下列不等式错误的是



 的展开式中含
的展开式中含  项的系数为12,则展开式的常数项为__________.
项的系数为12,则展开式的常数项为__________. 满足
满足 ,且
,且 (
( ),则数列
),则数列 的前10项和为 .
的前10项和为 . 中,
中, 是
是 中点,已知
中点,已知 .
.
 的三边长是连续三个正整数,求
的三边长是连续三个正整数,求 的余弦值.
的余弦值. .
. ;
; ,且
,且 ,求证:
,求证: .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号