某大学志愿者协会中，数学学院志愿者有8人，其中含5名男生，3名女生；外语学院志愿者有4人，其中含1名男生，3名女生．现采用分层抽样的方法（层内采用简单随机抽样）从两个学院中共抽取3名同学，到希望小学进行支教活动．
（1）求从数学学院抽取的同学中至少有1名女同学的概率；
（2）记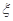
为抽取的
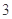名同学中男同学的人数，求随机变量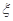的分布列和数学期望．
相关试题
．
的单调性；
，证明：当
时，
；
的图像与x轴交于A，B两点，线段AB中点的横坐标为x0，证明：
（x0）＜0．
上给定曲线
，试在此区间内确定点
的值，使图中所给阴影部分的面积
与
之和最小。
为实数，函数
.
，求
的最小值．
，
，
和
.
，作
，求
中，角A、B、C的对边分别为a、b、c，且
，
，
边上的中线
的长为
．
和角
的大小； 相关知识点
推荐套卷
某大学志愿者协会中，数学学院志愿者有8人，其中含5名男生，3名女生；外语学院志愿者有4人，其中含1名男生，3名女生．现采用分层抽样的方法（层内采用简单随机抽样）从两个学院中共抽取3名同学，到希望小学进行支教活动．
（1）求从数学学院抽取的同学中至少有1名女同学的概率；
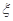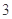（2）记为抽取的名同学中男同学的人数，求随机变量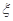的分布列和数学期望．
粤公网安备 44130202000953号