在建立两个变量的回归模型中,分别选择了4个不同的模型,他们的相关指数 如下,其中拟合得最好的模型为
如下,其中拟合得最好的模型为
A. 的模型1 的模型1 |
B. 的模型2 的模型2 |
C. 的模型3 的模型3 |
D. 的模型4 的模型4 |
(文)利用独立性检验来考虑两个分类变量X,Y是否有关系时,通过查阅前面所给表格断言“X和Y有关系”的可信度.如果我们有95%的把握认为“X和Y有关系”则( )
A.k 6.635 6.635 |
B.k 5.024 5.024 |
C.k 3.84 3.84 |
D.k 2.706 2.706 |
为了考察两个变量x和y之间的线性相关性,甲、乙两位同学各自独立地做10次和15次试验,并且利用线性回归方法,求得回归直线分别为l1和l2,已知两个人在试验中发现对变量x的观测数据的平均值都是s,对变量y的观测数据的平均值都是t,那么下列说法正确的是 ( )
| A.l1和l2必定平行 | B.l1和l2有交点(s,t) |
| C.l1与l2必定重合 | D.l1与l2相交,但交点不一定是(s,t) |
某商品销售量y(件)与销售价格x(元/件)
负相关,则其回归方程可能是 ( )
A.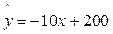 |
B. |
C. |
D.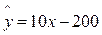 |
某校数学组为了选修课的设置,在设置的所有科目中随机抽取了30门,用问卷调查的方式对两个班的学生进行了普查。经统计,每一门选修课受学生喜欢的人次数如茎叶图所示。
如果要在这30门选出4门确立为选修课,并使得其中恰好有3门选修课受学生的喜欢人次数在[50,100]的概率是( )
A. |
B. |
C. |
D. |
在一次实验中,测得(x,y)的四组值分别为(1,2),(2,3),(3,4),(4,5),则y与x的线性回归方程可能是( )
A.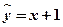 |
B.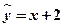 |
C. |
D. |
甲、乙两名同学在5次体育测试中的成绩统计的茎叶图如图所示,若甲、乙两人的平均成绩分别是 、
、 ,则下列结论正确的是( )
,则下列结论正确的是( )
A. < < ;乙比甲成绩稳定 ;乙比甲成绩稳定 |
|
B. > > ;甲比乙成绩稳定 ;甲比乙成绩稳定 |
C. > > ;乙比甲成绩稳定 ;乙比甲成绩稳定 |
D. < < ;甲比乙成绩稳定 ;甲比乙成绩稳定 |
右图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则在这几场比赛得分中甲的中位数与乙的众数之和是( )
| A.50 | B.41 | C.51 | D.61.5 |

某研究小组在一项实验中获得一组数据,将其整理得到如图所示的散点图,下列函数中,最能近似刻画y与t之间关系的是( )
A. |
B.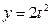 |
C. |
D.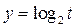 |
某赛季,甲、乙两名篮球运动员都参加了11场比赛,他们每场比赛得分的情况用如图所示的茎叶图表示,则甲、乙两名运动员的中位数分别是 ( ※ )
A. 、 、 |
B. 、 、 |
C. 、 、 |
D. 、 、 |

某化工产品的产量受a、b、c三个因素的影响,每个因素有两个水平,分别用a1,a2,b1,b2,c1,c2表示.分析如右正交试验结果表,对试验结果影响最大的因素是( )
| A. a | B. b | C. c | D.不能确定 |
| 实验号 列 号 |
a |
b |
c |
实验结果 |
| 1 |
a1 |
b1 |
c1 |
79 |
| 2 |
a1 |
b2 |
c2 |
65 |
| 3 |
a2 |
b1 |
c2 |
88 |
| 4 |
a2 |
b2 |
c1 |
81 |
| 1水平的平均值 |
72 |
83.5 |
80 |
|
| 2水平的平均值 |
84.5 |
73 |
76.5 |
|