一名小学生的年龄和身高(单位:cm)的数据如下表:

由散点图可知,身高 与年龄
与年龄 之间的线性回归方程为
之间的线性回归方程为 ,则
,则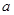 的值为( )
的值为( )
| A.65 | B.74 | C.56 | D.47 |
汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲,乙,丙三辆汽车在不同速度下的燃油效率情况,下列叙述中正确的是( )

| A.消耗1升汽油,乙车最多可行驶5千米 |
| B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多 |
| C.甲车以80千米/小时的速度行驶1小时,消耗10升汽油 |
| D.某城市机动车最高限速80千米/小时,相同条件下,在该市用丙车比用乙车更省油 |
设某中学的女生体重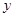 (kg)与身高
(kg)与身高 (cm)具有线性相关关系,根据一组样本数
(cm)具有线性相关关系,根据一组样本数
 ,用最小二乘法建立的线性回归直线方程为
,用最小二乘法建立的线性回归直线方程为 ,给出下列结论,则错误的是( )
,给出下列结论,则错误的是( )
A.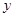 与 与 具有正的线性相关关系 具有正的线性相关关系 |
| B.若该中学某女生身高增加1cm,则其体重约增加0.85kg |
C.回归直线至少经过样本数据  中的一个 中的一个 |
D.回归直线一定过样本点的中心点 |
为了解某商品销售量 (单位:件)与销售价格
(单位:件)与销售价格 (单位:元/件)的关系,统计了(
(单位:元/件)的关系,统计了( )的10组值,并画成散点图如图,则其回归方程可能是
)的10组值,并画成散点图如图,则其回归方程可能是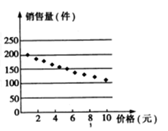
A. |
B.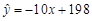 |
C.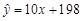 |
D. |
下列判断中不正确的是( )
A. 为变量间的相关系数, 为变量间的相关系数, 值越大,线性相关程度越高 值越大,线性相关程度越高 |
| B.在平面直角坐标系中,可以用散点图发现变量之间的变化规律 |
C.线性回归方程代表了观测值 、 、 之间的关系 之间的关系 |
| D.任何一组观测值都能得到具有代表意义的回归直线方程 |
某产品的广告费用x与销售额y的统计数据如下表:根据上表可得回归方程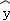 =
= x+a中的b=10.6,据此模型预报广告费用为10万元时销售额为( )
x+a中的b=10.6,据此模型预报广告费用为10万元时销售额为( )
| 广告费用x(万元) |
4 |
2 |
3 |
5 |
| 销售额y(万元) |
49 |
26 |
39 |
58 |
A.112.1万元 B.113.1万元 C.111.9万元 D.113.9万元
某产品的广告费用x与销售额y的统计数据如下表:根据上表可得回归方程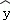 =
=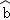 x+a中的b=10.6,据此模型预报广告费用为10万元时销售额为( )
x+a中的b=10.6,据此模型预报广告费用为10万元时销售额为( )
| 广告费用x(万元) |
4 |
2 |
3 |
5 |
| 销售额y(万元) |
49 |
26 |
39 |
58 |
A.112.1万元 B.113.1万元 C.111.9万元 D.113.9万元
某产品的广告费用x与销售额y的统计数据如下表:
| 广告费用x(万元) |
3 |
4 |
5 |
6 |
| 销售额y(万元) |
25 |
30 |
40 |
45 |
根据上表可得回归方程 =
= x+
x+ ,其中
,其中 为7,据此模型,若广告费用为10万元,预报销售额等于( )
为7,据此模型,若广告费用为10万元,预报销售额等于( )
A.42.0万元 B.57.0万元
C.66.5万元 D.73.5万元
对于下列表格所示的五个散点,已知求得的线性回归直线方程为 =0.8x-155.
=0.8x-155.
| x |
196 |
197 |
200 |
203 |
204 |
| y |
1 |
3 |
6 |
7 |
m |
则实数m的值为( )
A.8.4 B.8.2 C.8 D.8.5
对变量 ,
,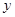 观测数据
观测数据 ,得散点图
,得散点图 ;对变量
;对变量 ,
, 有观测数据
有观测数据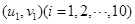 ,得散点图
,得散点图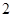 .由这两个散点图可以判断( )
.由这两个散点图可以判断( )

A.变量 与 与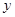 正相关, 正相关, 与 与 正相关 正相关 |
B.变量 与 与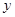 正相关, 正相关, 与 与 负相关 负相关 |
C.变量 与 与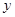 负相关, 负相关, 与 与 正相关 正相关 |
D.变量 与 与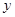 负相关, 负相关, 与 与 负相关 负相关 |
已知x,y的取值如下表示:若y与x线性相关,且 ,则a=( )
,则a=( )
| x |
0 |
1 |
3 |
4 |
| y |
2.2 |
4.3 |
4.8 |
6.7 |
A.2.2 B.2.6 C.2.8 D.2.9