某校数学组为了选修课的设置，在设置的所有科目中随机抽取了30门，用问卷调查的方式对两个班的学生进行了普查。经统计，每一门选修课受学生喜欢的人次数如茎叶图所示。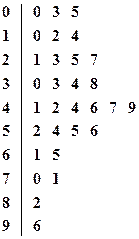
如果要在这30门选出4门确立为选修课，并使得其中恰好有3门选修课受学生的喜欢人次数在[50，100]的概率是（ ）
A． |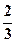
B． |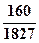
C． |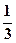
D． |
是纯虚数，则
等于（）
是两条不同的直线，
是三个不同的平面，则下列命题中的真命题是（）
，则
，
，则
，
，则
满足
，下列不等式中正确的是（）
：
与圆
：
位置关系是（）
的零点所在的一个区间是（）
相关知识点
推荐套卷
某校数学组为了选修课的设置，在设置的所有科目中随机抽取了30门，用问卷调查的方式对两个班的学生进行了普查。经统计，每一门选修课受学生喜欢的人次数如茎叶图所示。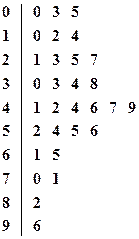
如果要在这30门选出4门确立为选修课，并使得其中恰好有3门选修课受学生的喜欢人次数在[50，100]的概率是（ ）
| A． |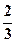
B． |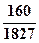
C． |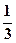
D． |
粤公网安备 44130202000953号