(本小题满分14分)已知{an}是等差数列,其前n项的和为Sn,{bn}是等比数列,且a1=b1=2,a4+b4=21,S4+b4=30.
(1)求数列{an}和{bn}的通项公式;
(2)记cn=anbn,n∈N*,求数列{cn}的前n项和.
设等差数列{an}满足a3=5,a10=-9.
(1)求{an}的通项公式;
(2)求{an}的前n项和Sn及使得Sn最大的序号n的值.
本题共有3个小题,第1小题4分,第2小题5分,第3小题5分.
设等比数列 的前
的前 项的和为
项的和为 ,公比为
,公比为 .
.
(1)若 成等差数列,求证:
成等差数列,求证: 成等差数列;
成等差数列;
(2)若 (
( 为互不相等的正整数)成等差数列,试问数列
为互不相等的正整数)成等差数列,试问数列 中是否存在不同的三项成等差数列?若存在,写出两组这三项;若不存在,请说明理由;
中是否存在不同的三项成等差数列?若存在,写出两组这三项;若不存在,请说明理由;
(3)若 为大于
为大于 的正整数.试问
的正整数.试问 中是否存在一项
中是否存在一项 ,使得
,使得 恰好可以表示为该数列中连续两项的和?请说明理由.
恰好可以表示为该数列中连续两项的和?请说明理由.
(本小题满分12分)
已知实数 ,且
,且 依次成等差数列,
依次成等差数列,
(1)求实数 的值;
的值;
(2)若数列 满足
满足 求
求 的通项公式;
的通项公式;
(3)在(2)的条件下,是否存在实数 ,对任意
,对任意 ,不等式
,不等式 恒成立,若存在,求
恒成立,若存在,求 的取值范围;否则说明理由.
的取值范围;否则说明理由.
已知各项均不相等的等差数列 的前五项和
的前五项和 ,且
,且 成等比数列.
成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)设 为数列
为数列 的前
的前 项和,若存在
项和,若存在 ,使得
,使得 成立.
成立.
求实数 的取值范围.
的取值范围.
(本小题满分15分)等差数列 中,
中, ,
, .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
(本小题满分12分)
已知 为等差数列,
为等差数列, 为
为 的前
的前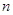 项和,且
项和,且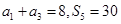 .
.
(1)求 的通项公式;(2)若
的通项公式;(2)若 成等比数列,求正整数
成等比数列,求正整数 的值.
的值.