数列 为公差不为
为公差不为 的等差数列,
的等差数列, 为前
为前 项和,
项和, 和
和 的等差中项为
的等差中项为 ,且
,且 .令
.令 数列
数列 的前
的前 项和为
项和为 .
.
(Ⅰ)求 及
及 ;
;
(Ⅱ)是否存在正整数 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知两个动点 、
、 和一个定点
和一个定点 均在抛物线
均在抛物线 上(
上( 、
、 与
与 不重合). 设
不重合). 设 为抛物线的焦点,
为抛物线的焦点, 为其对称轴上一点,若
为其对称轴上一点,若 ,且
,且 、
、 、
、 成等差数列.
成等差数列.
(Ⅰ)求 的坐标(可用
的坐标(可用 、
、 和
和 表示);
表示);
(Ⅱ)若 ,
, ,
, 、
、 两点在抛物线
两点在抛物线 的准线上的射影分别为
的准线上的射影分别为 、
、 ,求四边形
,求四边形 面积的取值范围.
面积的取值范围.
以下命题正确的是: .
①把函数 的图象向右平移
的图象向右平移 个单位,可得到
个单位,可得到 的图象;
的图象;
②四边形 为长方形,
为长方形, 为
为 中点,在长方形
中点,在长方形 内随机取一点
内随机取一点 ,取得的
,取得的 点到
点到 的距离大于1的概率为
的距离大于1的概率为 ;
;
③等差数列 前
前 项和为
项和为 ,则三点
,则三点 ,
, ,
, 共线;
共线;
④已知 是定义在
是定义在 上的函数
上的函数 的导函数,且满足
的导函数,且满足 ,则不等式
,则不等式 的解集为
的解集为 .
.
设等差数列{an}的公差为d,点(an,bn)在函数f (x)=2x的图象上(n∈N*).
(Ⅰ)证明:数列{bn}为等比数列;
(Ⅱ)若a1=1,直线y=(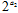 ln2)(x-a2)+
ln2)(x-a2)+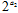 在x轴上的截距为2-
在x轴上的截距为2-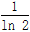 ,求数列{anb
,求数列{anb }的前n项和Sn.
}的前n项和Sn.
数列 、
、 满足
满足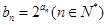 ,则“数列
,则“数列 是等差数列”是“数列
是等差数列”是“数列 是等比数列”的()
是等比数列”的()
| A.充分但不必要条件 | B.必要但不充分条件 |
| C.充要条件 | D.既不充分也必要条件 |
已知等比数列 是递增数列,
是递增数列,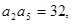
 ,数列
,数列 满足
满足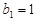 ,且
,且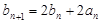 (
(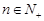 )
)
(1)证明:数列 是等差数列;
是等差数列;
(2)若对任意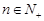 ,不等式
,不等式 总成立,求实数
总成立,求实数 的最大值.
的最大值.
在正项数列{an}中,a1=1,点An( )在曲线y2﹣x2=1上,数列{bn}中,点(bn,Tn)在直线y=﹣
)在曲线y2﹣x2=1上,数列{bn}中,点(bn,Tn)在直线y=﹣ x+1上,其中Tn是数列{bn}的前n项和.
x+1上,其中Tn是数列{bn}的前n项和.
(1)求数列{an},{bn}的通项公式an,bn;
(2)若cn=an•bn,数列{cn}的前n项和Sn.