已知函数f(x)=ln(x+1)-x2-x.
(1)若关于x的方程f(x)=- x+b在区间[0,2]上恰有两个不同的实数根,求实数b的取值范围;
x+b在区间[0,2]上恰有两个不同的实数根,求实数b的取值范围;
(2)证明:对任意的正整数n,不等式2+ +
+ +…+
+…+ >ln(n+1)都成立.
>ln(n+1)都成立.
设椭圆M: =1(a>
=1(a> )的右焦点为F1,直线l:x=
)的右焦点为F1,直线l:x= 与x轴交于点A,若
与x轴交于点A,若 =2
=2 (其中O为坐标原点).
(其中O为坐标原点).
(1)求椭圆M的方程;
(2)设P是椭圆M上的任意一点,EF为圆N:x2+(y-2)2=1的任意一条直径(E,F为直径的两个端点),求 ·
· 的最大值.
的最大值.
在平面直角坐标系xOy中,已知圆x2+y2-12x+32=0的圆心为Q,过点P(0,2)且斜率为k的直线l与圆Q相交于不同的两点A,B.
(1)求圆Q的面积;
(2)求k的取值范围;
(3)是否存在常数k,使得向量 +
+ 与
与 共线?如果存在,求k的值;如果不存在,请说明理由.
共线?如果存在,求k的值;如果不存在,请说明理由.
已知数列{an}满足a1=a(a>0,a∈N*),a1+a2+…+an-pan+1=0(p≠0,p≠-1,n∈N*).
(1)求数列{an}的通项公式an;
(2)若对每一个正整数k,若将ak+1,ak+2,ak+3按从小到大的顺序排列后,此三项均能构成等差数列,且公差为dk.①求p的值及对应的数列{dk}.
②记Sk为数列{dk}的前k项和,问是否存在a,使得Sk<30对任意正整数k恒成立?若存在,求出a的最大值;若不存在,请说明理由.
设函数 ,其中
,其中 .
.
(1)当 时,求不等式
时,求不等式 的解集;
的解集;
(2)若不等式 的解集为
的解集为 ,求
,求 的值.
的值.
数列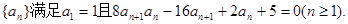 记
记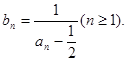
(1)求b1、b2、b3、b4的值;
(2)求数列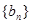 的通项公式及数列
的通项公式及数列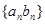 的前n项和
的前n项和
如图,已知椭圆 的离心率是
的离心率是 ,
, 分别是椭圆
分别是椭圆 的左、右两个顶点,点
的左、右两个顶点,点 是椭圆
是椭圆 的右焦点。点
的右焦点。点 是
是 轴上位于
轴上位于 右侧的一点,且满足
右侧的一点,且满足 .
.
(1)求椭圆 的方程以及点
的方程以及点 的坐标;
的坐标;
(2)过点 作
作 轴的垂线
轴的垂线 ,再作直线
,再作直线 与椭圆
与椭圆 有且仅有一个公共点
有且仅有一个公共点 ,直线
,直线 交直线
交直线 于点
于点 .求证:以线段
.求证:以线段 为直径的圆恒过定点,并求出定点的坐标.
为直径的圆恒过定点,并求出定点的坐标.
如图,在 中,
中, ,
, ,点
,点 在边
在边 上,设
上,设 ,过点
,过点 作
作 交
交 于
于 ,作
,作 交
交 于
于 。沿
。沿 将
将 翻折成
翻折成 使平面
使平面 平面
平面 ;沿
;沿 将
将 翻折成
翻折成 使平面
使平面 平面
平面 .
.
(1)求证: 平面
平面 ;
;
(2)是否存在正实数 ,使得二面角
,使得二面角 的大小为
的大小为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
设函数f(x),g(x)的定义域分别为M,N,且M是N真子集,若对任意的x∈M,都有g(x)=f(x),则称g(x)是f(x)的“拓展函数”.已知函数f(x)=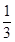 log2x,若g(x)是f(x)的“拓展函数”,且g(x)是偶函数,则符合条件的一个g(x)的解析式是________.
log2x,若g(x)是f(x)的“拓展函数”,且g(x)是偶函数,则符合条件的一个g(x)的解析式是________.
如图,在直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB= AB.
AB.
(1)证明:BC1∥平面A1CD;
(2)求二面角D-A1C-E的正弦值.
已知曲线C1的参数方程为 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sin θ.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sin θ.
(1)把C1的参数方程化为极坐标方程;
(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π).
如图,点P(0,-1)是椭圆C1: =1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径.l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A,B两点,l2交椭圆C1于另一点D.
=1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径.l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A,B两点,l2交椭圆C1于另一点D.
(1)求椭圆C1的方程;
(2)求△ABD面积取最大值时直线l1的方程.
若两个椭圆的离心率相等,则称它们为“相似椭圆”.如图,在直角坐标系xOy中,已知椭圆C1: =1,A1,A2分别为椭圆C1的左、右顶点.椭圆C2以线段A1A2为短轴且与椭圆C1为“相似椭圆”.
=1,A1,A2分别为椭圆C1的左、右顶点.椭圆C2以线段A1A2为短轴且与椭圆C1为“相似椭圆”.
(1)求椭圆C2的方程;
(2)设P为椭圆C2上异于A1,A2的任意一点,过P作PQ⊥x轴,垂足为Q,线段PQ交椭圆C1于点H.求证:H为△PA1A2的垂心.(垂心为三角形三条高的交点)
已知椭圆C: =1(a>b>0)上任一点P到两个焦点的距离的和为2
=1(a>b>0)上任一点P到两个焦点的距离的和为2 ,P与椭圆长轴两顶点连线的斜率之积为-
,P与椭圆长轴两顶点连线的斜率之积为- .设直线l过椭圆C的右焦点F,交椭圆C于两点A(x1,y1),B(x2,y2).
.设直线l过椭圆C的右焦点F,交椭圆C于两点A(x1,y1),B(x2,y2).
(1)若 =
= (O为坐标原点),求|y1-y2|的值;
(O为坐标原点),求|y1-y2|的值;
(2)当直线l与两坐标轴都不垂直时,在x轴上是否总存在点Q,使得直线QA,QB的倾斜角互为补角?若存在,求出点Q坐标;若不存在,请说明理由.
如图,椭圆 =1(a>b>0)的上,下两个顶点为A,B,直线l:y=-2,点P是椭圆上异于点A,B的任意一点,连接AP并延长交直线l于点N,连接PB并延长交直线l于点M,设AP所在的直线的斜率为k1,BP所在的直线的斜率为k2.若椭圆的离心率为
=1(a>b>0)的上,下两个顶点为A,B,直线l:y=-2,点P是椭圆上异于点A,B的任意一点,连接AP并延长交直线l于点N,连接PB并延长交直线l于点M,设AP所在的直线的斜率为k1,BP所在的直线的斜率为k2.若椭圆的离心率为 ,且过点A(0,1).
,且过点A(0,1).
(1)求k1·k2的值;
(2)求MN的最小值;
(3)随着点P的变化,以MN为直径的圆是否恒过定点?若过定点,求出该定点;如不过定点,请说明理由.