高考数学（文）二轮复习专题提升训练江苏专用阶段检测4练习卷

已知过A(－1，a)，B(a,8)两点的直线与直线2x－y＋1＝0平行，则a的值为________．

圆(x＋2)²＋y²＝4与圆(x－2)²＋(y－1)²＝9的位置关系为________．

已知圆(x＋1)²＋(y－1)²＝1上一点P到直线3x－4y－3＝0距离为d，则d的最小值为________．

已知圆x²＋y²－4x－9＝0与y轴的两个交点A，B都在某双曲线上，且A，B两点恰好将此双曲线的焦距三等分，则此双曲线的标准方程为________．

已知双曲线＝1(a>0，b>0)的渐近线方程为y＝±x，则它的离心率为________．

椭圆＝1(a＞b＞0)的左、右焦点分别是F₁、F₂，过F₁作倾斜角为45°的直线与椭圆的一个交点为M，若MF₂垂直于x轴，则椭圆的离心率为________．

设圆C的圆心与双曲线＝1(a>0)的右焦点重合，且该圆与此双曲线的渐近线相切，若直线l：x－y＝0被圆C截得的弦长等于2，则a的值为________．

设圆x²＋y²＝1的一条切线与x轴、y轴分别交于点A、B，则线段AB长度的最小值为________．

已知圆O的方程为x²＋y²＝2，圆M的方程为(x－1)²＋(y－3)²＝1，过圆M上任一点P作圆O的切线PA，若直线PA与圆M的另一个交点为Q，则当弦PQ的长度最大时，直线PA的斜率是________．

设F是双曲线＝1的右焦点，双曲线两条渐近线分别为l₁，l₂，过F作直线l₁的垂线，分别交l₁，l₂于A、B两点．若OA，AB，OB成等差数列，且向量与同向，则双曲线离心率e的大小为________．

已知点P(x，y)是直线kx＋y＋4＝0(k>0)上一动点，PA，PB是圆C：x²＋y²－2y＝0的两条切线，A，B为切点，若四边形PACB的最小面积是2，则k的值为________．

双曲线C：x²－y²＝1，若双曲线C的右顶点为A，过A的直线l与双曲线C的两条渐近线交于P，Q两点，且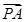＝2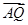，则直线l的斜率为________．

设圆x²＋y²＝2的切线l与x轴正半轴、y轴正半轴分别交于点A，B，当|AB|取最小值时，切线l的方程为________．

设双曲线－y²＝1的右焦点为F，点P₁、P₂、…、P_n是其右上方一段(2≤x≤2 ，y≥0)上的点，线段|P_kF|的长度为a_k(k＝1,2,3，…，n)．若数列{a_n}成等差数列且公差d∈，则n的最大取值为________．

已知中心在坐标原点O的椭圆C经过点A(2,3)，且点F(2,0)为其右焦点．
(1)求椭圆C的方程；
(2)是否存在平行于OA的直线l，使得直线l与椭圆C有公共点，且直线OA与l的距离等于4？若存在，求出直线l的方程；若不存在，请说明理由．

已知椭圆C：＝1(a＞b＞0)的离心率为，一条准线l：x＝2.
(1)求椭圆C的方程；
(2)设O为坐标原点，M是l上的点，F为椭圆C的右焦点，过点F作OM的垂线与以OM为直径的圆D交于P，Q两点．
①若PQ＝，求圆D的方程；
②若M是l上的动点，求证点P在定圆上，并求该定圆的方程．

在平面直角坐标系xOy中，已知圆x²＋y²－12x＋32＝0的圆心为Q，过点P(0,2)且斜率为k的直线l与圆Q相交于不同的两点A，B.
(1)求圆Q的面积；
(2)求k的取值范围；
(3)是否存在常数k，使得向量＋与共线？如果存在，求k的值；如果不存在，请说明理由．

如图，在平面直角坐标系xOy中，椭圆C：＝1(a>b>0)的离心率为，以坐标原点为圆心，椭圆C的短半轴长为半径的圆与直线x－y＋2＝0相切．

(1)求椭圆C的方程；
(2)已知点P(0,1)，Q(0,2)，设M，N是椭圆C上关于y轴对称的不同两点，直线PM与QN相交于点T.求证：点T在椭圆C上．

已知直线l：y＝x＋，圆O：x²＋y²＝5，椭圆E：＝1(a>b>0)的离心率e＝，直线l被圆O截得的弦长与椭圆的短轴长相等．
(1)求椭圆E的方程；
(2)过圆O上任意一点P作椭圆E的两条切线，若切线都存在斜率，求证：两条切线的斜率之积为定值．

设椭圆M：＝1(a>)的右焦点为F₁，直线l：x＝与x轴交于点A，若＝2 (其中O为坐标原点)．
(1)求椭圆M的方程；
(2)设P是椭圆M上的任意一点，EF为圆N：x²＋(y－2)²＝1的任意一条直径(E，F为直径的两个端点)，求·的最大值．