几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了"解数学题获取软件激活码"的活动.这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是2 0,接下来的两项是2 0,2 1,再接下来的三项是2 0,2 1,2 2,依此类推.求满足如下条件的&最小整数
且该数列的前N项和为2的整数幂.那么该款软件的激活码是( )
A.440B.330C.220D.110
已知F为抛物线
的焦点,过F作两条互相垂直的直线l 1,l 2,直线l 1与C交于A、B两点,直线l 2与C交于D、E两点,则
的最小值为( )
A.16B.14C.12D.10
已知曲线
,
,则下面结论正确的是( )
A.把 C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移 个单位长度,得到曲线 C 2
B.把 C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移 个单位长度,得到曲线 C 2
C.把 C 1上各点的横坐标缩短到原来的 倍,纵坐标不变,再把得到的曲线向右平移 个单位长度,得到曲线 C 2
D.把 C 1上各点的横坐标缩短到原来的 倍,纵坐标不变,再把得到的曲线向左平移 个单位长度,得到曲线 C 2
右面程序框图是为了求出满足
的最小偶数
,那么在  和
和  两个空白框中,可以分别填入( )
两个空白框中,可以分别填入( )
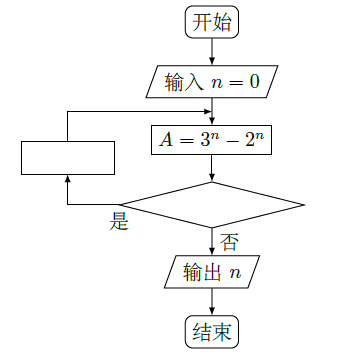
A. 和
B. 和
C. 和
D. 和
某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( )
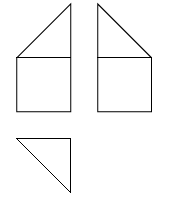
| A. | 10 |
B. | 12 |
C. | 14 |
D. | 16 |
函数
在
单调递减,且为奇函数.若
,则满足
的
的取值范围是( )
A. B. C. D.
记
为等差数列
的前
项和.若
,
,则
的公差为( )
A.1B.2C.4D.8
设有下面四个命题
:若复数 满足 ,则 ;
:若复数 满足 ,则 ;
:若复数 满足 ,则 ;
:若复数 ,则 .
其中的真命题为( )
A. B. C. D.
如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( )
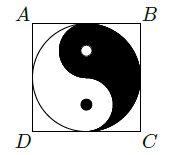
| A. |
|
B. |
|
| C. |
|
D. |
|
设O为坐标原点,动点M在椭圆
上,过M做x轴的垂线,垂足为N,点P满足
.
(1) 求点 P的轨迹方程;
(2) 设点 Q在直线 上,且 .证明:过点 P且垂直于 的直线 l过 C的左焦点 F.