如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为y= ,在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O′B′.设P(t,0),当O′B′与双曲线有交点时,t的取值范围是 .
,在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O′B′.设P(t,0),当O′B′与双曲线有交点时,t的取值范围是 .

已知反比例函数y1=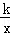 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2).
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2).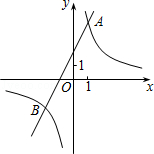
(1)求这两个函数的关系式;
(2)观察图象,直接写出使y1>y2成立的自变量x的取值范围.
当x>0时,函数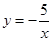 的图象在( )
的图象在( )
| A.第四象限 | B.第三象限 | C.第二象限 | D.第一象限 |
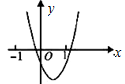
二次函数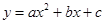 的图象如图所示,反比例函数
的图象如图所示,反比例函数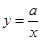 与正比例函数
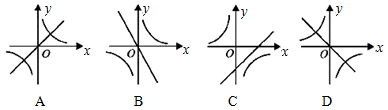
与正比例函数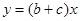 在同一坐标系中的大致图象可能是( )
在同一坐标系中的大致图象可能是( )
已知:如图,在平面直角坐标系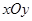 中,直线AB分别与
中,直线AB分别与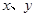 轴交于点B、A,与反比例函数的图象分别交于点C、D,
轴交于点B、A,与反比例函数的图象分别交于点C、D,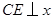 轴于点E,
轴于点E,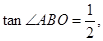
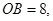
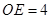 .求该反比例函数的解析式.
.求该反比例函数的解析式.
在函数 (
(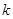 为常数)图象上有三个点(-2,y1),(-1,y2),(
为常数)图象上有三个点(-2,y1),(-1,y2),( ,y3),函数值y1,y2,y3的大小关系为 .(用“<”连接)
,y3),函数值y1,y2,y3的大小关系为 .(用“<”连接)
下列各点中,在函数 的图象上的点是( )
的图象上的点是( )
| A.(1,0.5) | B.(2,-1) |
| C.(-1,-2) | D.(-2,1) |
如图,在直角梯形OABC中,BC∥AO,∠AOC=90°,点A,B的坐标分别为(5,0),(2,6),点D为AB上一点,且BD=2AD,曲线 (k>0)经过点D,交BC于点E.
(k>0)经过点D,交BC于点E.
(1)求曲线的解析式;
(2)求四边形ODBE的面积.
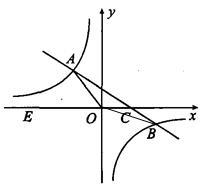
如图在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=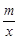 (m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=
(m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=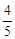 .
.
(1)求该反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)直接写出不等式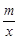 ﹤kx+b的x的取值范围.
﹤kx+b的x的取值范围.
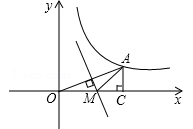
如图,点A(3,n)在双曲线y= 上,过点A作AC⊥x轴,垂足为C.线段OA的垂直平分线交OC于点M,则△AMC周长的值是( )
上,过点A作AC⊥x轴,垂足为C.线段OA的垂直平分线交OC于点M,则△AMC周长的值是( )
A.3 B.4 C.5 D.6