某公司投入研发费用80万元 万元只计入第一年成本),成功研发出一种产品.公司按订单生产(产量 销售量),第一年该产品正式投产后,生产成本为6元 件.此产品年销售量 (万件)与售价 (元 件)之间满足函数关系式 .
(1)求这种产品第一年的利润 (万元)与售价 (元 件)满足的函数关系式;
(2)若该产品第一年的利润为20万元,那么该产品第一年的售价是多少?
(3)在(2)的条件下,第二年,该公司将第一年的利润20万元 万元只计入第二年成本)再次投入研发,使产品的生产成本降为5元 件.为保持市场占有率,公司规定第二年产品售价不超过第一年的售价,另外受产能限制,销售量无法超过12万件.请计算该公司第二年的利润 至少为多少万元.
为积极响应新旧动能转换,提高公司经济效益,某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为40万元时,年销售量为600台;每台售价为45万元时,年销售量为550台.假定该设备的年销售量 (单位:台)和销售单价 (单位:万元)成一次函数关系.
(1)求年销售量 与销售单价 的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于70万元,如果该公司想获得10000万元的年利润,则该设备的销售单价应是多少万元?
今年,我市某中学响应习总书记“足球进校园”的号召,开设了“足球大课间”活动,现需要购进100个某品牌的足球供学生使用.经调查,该品牌足球2015年单价为200元,2017年单价为162元.
(1)求2015年到2017年该品牌足球单价平均每年降低的百分率;
(2)选购期间发现该品牌足球在两个文体用品商场有不同的促销方案:

试问去哪个商场购买足球更优惠?
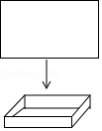
工人师傅用一块长为 ,宽为 的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)
(1)在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求长方体底面面积为 时,裁掉的正方形边长多大?
(2)若要求制作的长方体的底面长不大于底面宽的五倍,并在容器外表面进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,裁掉的正方形边长多大时,总费用最低,最低为多少?
列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按480元销售时,每天可销售160个;若销售单价每降低1元,每天可多售出2个.已知每个玩具的固定成本为360元,问这种玩具的销售单价为多少元时,厂家每天可获利润20000元?
某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量 (本 与每本纪念册的售价 (元 之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)请直接写出 与 的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为 元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
为满足市场需求,新生活超市在端午节前夕购进价格为3元 个的某品牌粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子售价不能超过进价的 ,请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.
2015年某县 总量为1000亿元,计划到2017年全县 总量实现1210亿元的目标.如果每年的平均增长率相同,那么该县这两年 总量的平均增长率为
A. B. C. D.
某地2014年为做好“精准扶贫”,投入资金1280万元用于异地安置,并规划投入资金逐年增加,2016年在2014年的基础上增加投入资金1600万元.
(1)从2014年到2016年,该地投入异地安置资金的年平均增长率为多少?
(2)在2016年异地安置的具体实施中,该地计划投入资金不低于500万元用于优先搬迁租房奖励,规定前1000户(含第1000户)每户每天奖励8元,1000户以后每户每天补助5元,按租房400天计算,试求今年该地至少有多少户享受到优先搬迁租房奖励?
为解决消费者停车难的问题,某商场新建一小型轿车停车场,经测算,此停车场每天需固定支出的费用(包括设施维修费、管理人员工资等)为600元,为制定合理的收费标准,该商场对每天轿车停放辆次(每辆轿车每停放一次简称为“辆次” 与每辆轿车的收费情况进行调查,发现每辆次轿车的停车费定价不超过10元时,每天来此停放的轿车都为300辆次;若每辆次轿车的停车费定价超过10元,则每超过1元,每天来此停放的轿车就减少12辆次,设每辆次轿车的停车费 元(为便于结算,停车费 只取整数),此停车场的日净收入为 元(日净收入 每天共收停车费 每天固定的支出)回答下列问题:
(1)①当 时, 与 的关系式为: ;
②当 时, 与 的关系式为: ;
(2)停车场能否实现3000元的日净收入?如能实现,求出每辆次轿车的停车费定价,如不能实现,请说明理由;
(3)该商场要求此停车场既要吸引顾客,使每天轿车停放的辆次较多,又要有最大的日净收入,按此要求,每辆次轿车的停车费定价应定为多少元?此时最大日净收入是多少元?
某商场对某种商品进行销售,第 天的销售单价为 元 件,日销售量为 件,其中 , 分别是 ,且 为整数)的一次函数,销售情况如表:
销售第 天 |
第1天 |
第2天 |
第3天 |
第4天 |
|
第30天 |
销售单价 (元 件) |
49 |
48 |
47 |
46 |
|
20 |
日销售量 (件 |
45 |
50 |
55 |
60 |
|
190 |
(1)观察表中数据,分别直接写出 与 , 与 的函数关系式: , ;
(2)求商场销售该商品第几天时该商品的日销售额恰好为3600元?
(3)销售商品的第15天为儿童节,请问:在儿童节前(不包括儿童节当天)销售该商品第几天时该商品的日销售额最多?商场决定将这天该商品的日销售额捐献给儿童福利院,试求出商场可捐款多少元?
某超市销售一种成本为每台20元的台灯,规定销售单价不低于成本价,又不高于每台32元.销售中平均每月销售量 (台 与销售单价 (元 的关系可以近似地看做一次函数,如下表所示:
|
22 |
24 |
26 |
28 |
|
90 |
80 |
70 |
60 |
(1)请直接写出 与 之间的函数关系式;
(2)为了实现平均每月375元的台灯销售利润,这种台灯的售价应定为多少?这时每月应购进台灯多少个?
(3)设超市每月台灯销售利润为 (元 ,求 与 之间的函数关系式,当 取何值时, 的值最大?最大值是多少?
某网络经销商销售一款夏季时装,进价每件60元,售价每件130元,每天销售30件,每销售一件需缴纳网络平台管理费4元.未来30天,这款时装将开展“每天降价1元”的促销活动,即从第一天起每天的单价均比前一天降1元,通过市场调查发现,该时装单价每降1元,每天销售量增加5件,设第 天 且 为整数)的销量为 件.
(1)直接写出 与 的函数关系式;
(2)在这30天内,哪一天的利润是6300元?
(3)设第 天的利润为 元,试求出 与 之间的函数关系式,并求出哪一天的利润最大,最大利润是多少.
小李在景区销售一种旅游纪念品,已知每件进价为6元,当销售单价定为8元时,每天可以销售200件.市场调查反映:销售单价每提高1元,日销量将会减少10件,物价部门规定:销售单价不能超过12元,设该纪念品的销售单价为 (元 ,日销量为 (件 ,日销售利润为 (元 .
(1)求 与 的函数关系式.
(2)要使日销售利润为720元,销售单价应定为多少元?
(3)求日销售利润 (元 与销售单价 (元 的函数关系式,当 为何值时,日销售利润最大,并求出最大利润.