初中数学一元二次方程试题

某公司投入研发费用80万元 $(80$万元只计入第一年成本），成功研发出一种产品．公司按订单生产（产量 $=$销售量），第一年该产品正式投产后，生产成本为6元 $/$件．此产品年销售量 $y$（万件）与售价 $x$（元 $/$件）之间满足函数关系式 $y=-x+26$．

（1）求这种产品第一年的利润 $W_1$（万元）与售价 $x$（元 $/$件）满足的函数关系式；

（2）若该产品第一年的利润为20万元，那么该产品第一年的售价是多少？

（3）在（2）的条件下，第二年，该公司将第一年的利润20万元 $(20$万元只计入第二年成本）再次投入研发，使产品的生产成本降为5元 $/$件．为保持市场占有率，公司规定第二年产品售价不超过第一年的售价，另外受产能限制，销售量无法超过12万件．请计算该公司第二年的利润 $W_2$至少为多少万元．

一元二次方程 $y^2-y-\frac{3}{4}=0$配方后可化为 $($　　 $)$

A． ${(y+\frac{1}{2})}^2=1$B． ${(y-\frac{1}{2})}^2=1$C． ${(y+\frac{1}{2})}^2=\frac{3}{4}$D． ${(y-\frac{1}{2})}^2=\frac{3}{4}$

已知关于 $x$的方程 $(k-1)x^2-2\mathit{kx}+k-3=0$有两个相等的实根，则 $k$的值是　　．

已知 $x_1$， $x_2$是方程 $2x^2-3x-1=0$的两根，则 $x_1^2+x_2^2=$　　．

关于 $x$的一元二次方程 $(k+1)x^2-2x+1=0$有两个实数根，则 $k$的取值范围是 $($　　 $)$

A． $k⩾0$B． $k⩽0$C． $k<0$且 $k\ne -1$D． $k⩽0$且 $k\ne -1$

关于 $x$的方程 $2x^2-5x\sin A+2=0$有两个相等的实数根，其中 $\angle A$是锐角三角形 $\mathit{ABC}$的一个内角．

（1）求 $\sin A$的值；

（2）若关于 $y$的方程 $y^2-10y+k^2-4k+29=0$的两个根恰好是 $\mathit{\Delta ABC}$的两边长，求 $\mathit{\Delta ABC}$的周长．

为积极响应新旧动能转换，提高公司经济效益，某科技公司近期研发出一种新型高科技设备，每台设备成本价为30万元，经过市场调研发现，每台售价为40万元时，年销售量为600台；每台售价为45万元时，年销售量为550台．假定该设备的年销售量 $y$（单位：台）和销售单价 $x$（单位：万元）成一次函数关系．

（1）求年销售量 $y$与销售单价 $x$的函数关系式；

（2）根据相关规定，此设备的销售单价不得高于70万元，如果该公司想获得10000万元的年利润，则该设备的销售单价应是多少万元？

若 $x_1$， $x_2$是一元二次方程 $x^2+x-2=0$的两个实数根，则 $x_1+x_2+x_1{x}_2=$　　．

已知 $\alpha$， $\beta$是方程 $x^2-3x-4=0$的两个实数根，则 ${\alpha }^2+\mathit{\alpha \beta }-3\alpha$的值为　　．

若关于 $x$的一元二次方程 $k{x}^2-2x-1=0$有两个不相等的实数根，则实数 $k$的取值范围是 $($　　 $)$

A． $k>-1$B． $k>-1$且 $k\ne 0$C． $k<-1$D． $k<-1$或 $k=0$

已知关于 $x$的一元二次方程 $a{x}^2-2x-1=0$有两个不相等的实数根，则 $a$的取值范围是　　．

今年，我市某中学响应习总书记“足球进校园”的号召，开设了“足球大课间”活动，现需要购进100个某品牌的足球供学生使用．经调查，该品牌足球2015年单价为200元，2017年单价为162元．

（1）求2015年到2017年该品牌足球单价平均每年降低的百分率；

（2）选购期间发现该品牌足球在两个文体用品商场有不同的促销方案：

试问去哪个商场购买足球更优惠？

若 $x_1$， $x_2$是方程 $x^2-2\mathit{mx}+m^2-m-1=0$的两个根，且 $x_1+x_2=1-x_1{x}_2$，则 $m$的值为 $($　　 $)$

A． $-1$或2B．1或 $-2$C． $-2$D．1

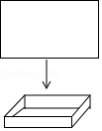
工人师傅用一块长为 $10\mathit{dm}$，宽为 $6\mathit{dm}$的矩形铁皮制作一个无盖的长方体容器，需要将四角各裁掉一个正方形．（厚度不计）

（1）在图中画出裁剪示意图，用实线表示裁剪线，虚线表示折痕；并求长方体底面面积为 $12d{m}^2$时，裁掉的正方形边长多大？

（2）若要求制作的长方体的底面长不大于底面宽的五倍，并在容器外表面进行防锈处理，侧面每平方分米的费用为0.5元，底面每平方分米的费用为2元，裁掉的正方形边长多大时，总费用最低，最低为多少？

若关于 $x$的一元二次方程 $k{x}^2-2x+1=0$有实数根，则 $k$的取值范围是　　．