高中数学多面角及多面角的性质试题

将函数f（x）=sin2x的图象向右平移φ（0＜φ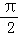＜）个单位后得到函数g（x）的图象．若对满足|f（x₁）﹣g（x₂）|=2的x₁、x₂，有|x₁﹣x₂|_min=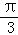，则φ=（ ）

A．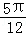

B．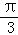

C．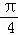

D．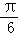

已知函数f（x）=（x∈R）．下列命题：
①函数f（x）既有最大值又有最小值；
②函数f（x）的图象是轴对称图形；
③函数f（x）在区间[﹣π，π]上共有7个零点；
④函数f（x）在区间（0，1）上单调递增．
其中真命题是        ．（填写出所有真命题的序号）

函数f（x）=sinπx+cosπx+|sinπx﹣cosπx|对任意x∈R有f（x₁）≤f（x）≤f（x₂）成立，则|x₂﹣x₁|的最小值为       ．

对于函数f（x）=sin²（x+）﹣cos²（x+），下列选项中正确的是（ ）

A．f（x）在（，）上是递增的

B．f（x）的图象关于原点对称

C．f（x）的最小正周期为2π

D．f（x）的最大值为2

已知函数f（x）=2sinωxcosωx﹣2sin²ωx+（ω＞0），直线x=x₁，x=x₂是函数y=f（x）的图象的任意两条对称轴，且|x₁﹣x₂|的最小值为．
（Ⅰ）求ω的值；
（Ⅱ）求函数f（x）的单调增区间；
（Ⅲ）若f（α）=，求sin（π﹣4α）的值．

函数f（x）=2sin（ωx+φ）的图象，其部分图象如图所示，则f（0）=      ．

已知函数f（x）=1+sinxcosx．
（1）求函数f（x）的最小正周期和单调递减区间；
（2）若tanx=2，求f（x）的值．

已知函数y=Asin（ωx+φ）+m的最大值是4，最小值是0，最小正周期，直线x=是其图象的一条对称轴，则下列各式中符合条件的解析式是（ ）

A．y=4sin（4x+）	B．y=2sin（4x+）+2
C．y=2sin（4x+）+2	D．y=2sin（2x+）+2

函数f（x）=cos（ωx+φ）的部分图象如图所示，则f（x）的单调递减区间为      ．

已知函数（ω＞0）的最小正周期为π．
（Ⅰ）求ω的值及函数f（x）的单调递增区间；
（Ⅱ）当时，求函数f（x）的取值范围．

函数f（x）=Asin（ωx+φ）（A＞0，ω＞0）的图象如图所示，则f（1）+f（2）+f（3）+…+f（2015）=      ．

将函数y=sin2x+cos2x的图象沿x轴向左平移φ个单位后，得到一个偶函数的图象，则|φ|的最小值为（ ）

A．

B．

C．

D．

设函数x．
（1）求f（x）的单调增区间；
（2）若x∈（0，4），求y=f（x）的值域．

将函数图象上每一点的横坐标变为原来的2倍（纵坐标不变），然后把所得图象上的所有点沿x轴向右平移个单位，得到函数y=2sinx的图象，则f（φ）=      ．

对于函数，现有下列命题：①函数是奇函数；②函数的最小正周期是；③点是函数的图象的一个对称中心；④函数在区间上单调递增，其中是真命题的为（   ）

A．②④

B．①④

C．②③

D．①③