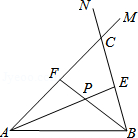
在线段 的同侧作射线 和 ,若 与 的平分线分别交射线 , 于点 , , 和 交于点 .如图,点点同学发现当射线 , 交于点 ;且 时,有以下两个结论:
① ;② .
那么,当 时:
(1)点点发现的结论还成立吗?若成立,请给予证明;若不成立,请求出 的度数,写出 , , 长度之间的等量关系,并给予证明;
(2)设点 为线段 上一点, ,若 ,四边形 的面积为 ,求 的长.
相关知识点
推荐套卷
在线段 的同侧作射线 和 ,若 与 的平分线分别交射线 , 于点 , , 和 交于点 .如图,点点同学发现当射线 , 交于点 ;且 时,有以下两个结论:
① ;② .
那么,当 时:
(1)点点发现的结论还成立吗?若成立,请给予证明;若不成立,请求出 的度数,写出 , , 长度之间的等量关系,并给予证明;
(2)设点 为线段 上一点, ,若 ,四边形 的面积为 ,求 的长.
