二次函数y=﹣x2+2x+m的图象与x轴交于A.B两点(B在A右侧),顶点为C,且A.B两点间的距离等于点C到x轴的距离的2倍.
(1)求此抛物线的解析式.
(2)求直线BC的解析式.
(3)若点P在抛物线的对称轴上,且⊙P与x轴以及直线BC都相切,求点P的坐标.
【提示:(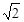 +1)(
+1)(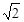 -1)=1】
-1)=1】
相关知识点
推荐套卷
二次函数y=﹣x2+2x+m的图象与x轴交于A.B两点(B在A右侧),顶点为C,且A.B两点间的距离等于点C到x轴的距离的2倍.
(1)求此抛物线的解析式.
(2)求直线BC的解析式.
(3)若点P在抛物线的对称轴上,且⊙P与x轴以及直线BC都相切,求点P的坐标.
【提示:(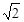 +1)(
+1)(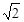 -1)=1】
-1)=1】