如图,⊙O的半径为6cm,射线PM与⊙O相切于点C,且PC=16cm.
(1)请你作出图中线段PC的垂直平分线EF,垂足为Q,并求出QO的长;
(2)在(1)的基础上画出射线QO,分别交⊙O于点A、B,将直线EF沿射线QM方向以5cm/s 的速度平移(平移过程中直线EF始终保持与PM垂直),设平移时间为t.当t为何值时,直线EF与⊙O相切?
(3)直接写出t为何值时,直线EF与⊙O无公共点?t为何值时,直线EF与⊙O有两个公共点?
相关知识点
推荐套卷
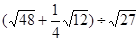
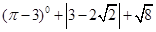
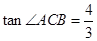 ,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且∠CEF=∠ACB.
,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且∠CEF=∠ACB.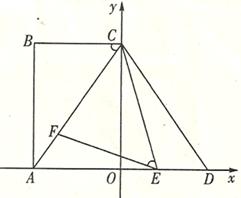
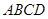 中,过
中,过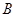 点作
点作 ,垂足为
,垂足为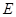 ,连结
,连结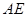 ,
,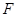 为
为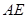 上一点,且
上一点,且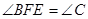 。
。 ∽△
∽△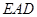 ;
;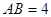 ,
,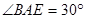 ,求
,求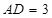 ,求
,求 的长.
的长.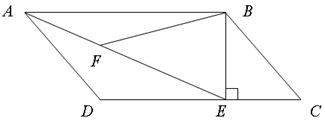

 粤公网安备 44130202000953号
粤公网安备 44130202000953号