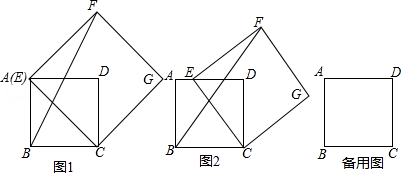
四边形 是边长为4的正方形，点 在边 所在直线上，连接 ，以 为边，作正方形 （点 ，点 在直线 的同侧），连接 ．
（1）如图1，当点 与点 重合时，请直接写出 的长；
（2）如图2，当点 在线段 上时， ；
①求点 到 的距离；
②求 的长；
（3）若 ，请直接写出此时 的长．
的值是正整数，求整数a．
．
．
，
，…
，试说明此猜想的正确性．（供参考：x3+y3=（x+y）（x2﹣xy+y2））
．相关知识点
推荐套卷
四边形 是边长为4的正方形，点 在边 所在直线上，连接 ，以 为边，作正方形 （点 ，点 在直线 的同侧），连接 ．
（1）如图1，当点 与点 重合时，请直接写出 的长；
（2）如图2，当点 在线段 上时， ；
①求点 到 的距离；
②求 的长；
（3）若 ，请直接写出此时 的长．
粤公网安备 44130202000953号