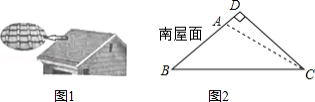
太阳能光伏建筑是现代绿色环保建筑之一，老张准备把自家屋顶改建

更新 2022-09-04
科目数学
题型解答题
难度中等
浏览 74

太阳能光伏建筑是现代绿色环保建筑之一，老张准备把自家屋顶改建成光伏瓦面，改建前屋顶截面 $ΔABC$ 如图2所示， $BC = 10$ 米， $∠ ABC = ∠ ACB = 36 °$ ，改建后顶点 $D$ 在 $BA$ 的延长线上，且 $∠ BDC = 90 °$ ，求改建后南屋面边沿增加部分 $AD$ 的长．（结果精确到0.1米）

（参考数据： $\sin 18 ° \approx 0.31$ ， $\cos 18 ° \approx 0.95$ ． $\tan 18 ° \approx 0.32$ ， $\sin 36 ° \approx 0.59$ ． $\cos 36 ° \approx 0.81$ ， $\tan 36 ° \approx 0.73)$

登录免费查看答案和解析

相关试题

如图，点 $P$ 是 $⊙ O$ 的直径 $AB$ 延长线上的一点 $(PB < OB)$ ，点 $E$ 是线段 $OP$ 的中点．

（1）尺规作图：在直径 $AB$ 上方的圆上作一点 $C$ ，使得 $EC = EP$ ，连接 $EC$ ， $PC$ （保留清晰作图痕迹，不要求写作法）；并证明 $PC$ 是 $⊙ O$ 的切线；

（2）在（1）的条件下，若 $BP = 4$ ， $EB = 1$ ，求 $PC$ 的长．

题型：未知
难度：未知

收藏答案/解析

为了做好校园疫情防控工作，校医每天早上对全校办公室和教室进行药物喷洒消毒，她完成3间办公室和2间教室的药物喷洒要 $19 \min$ ；完成2间办公室和1间教室的药物喷洒要 $11 \min$ ．

（1）校医完成一间办公室和一间教室的药物喷洒各要多少时间？

（2）消毒药物在一间教室内空气中的浓度 $y$ （单位： $mg / m^{3})$ 与时间 $x$ （单位： $\min)$ 的函数关系如图所示：校医进行药物喷洒时 $y$ 与 $x$ 的函数关系式为 $y = 2 x$ ，药物喷洒完成后 $y$ 与 $x$ 成反比例函数关系，两个函数图象的交点为 $A (m, n)$ ．当教室空气中的药物浓度不高于 $1 mg / m^{3}$ 时，对人体健康无危害，校医依次对一班至十一班教室（共11间）进行药物喷洒消毒，当她把最后一间教室药物喷洒完成后，一班学生能否进入教室？请通过计算说明．