2011年南京市六合区中考数学一模试卷
(本小题满分8分)
已知:如图,在△ABC中,AB=AC,DE∥BC,点F在边AC上,DF与BE相交 于点G,且∠EDF=∠ABE.
于点G,且∠EDF=∠ABE.
求证:(1)△DEF∽△BDE;
(2) .
.
(本小题满分10分)
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A= .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义,解下列问题:
(1)sad  的值为( )
的值为( )
A. |
B.1 | C. |
D.2 |
(2)对于 ,∠A的正对值sad A的取值范围是 .
,∠A的正对值sad A的取值范围是 .
(3)已知 ,其中
,其中 为锐角,试求sad
为锐角,试求sad 的值.
的值.
(本小题满分10分)
甲乙两车同时从A地出发,以各自的速度匀速向B地行驶.甲车先到达B地,停留一小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为60km/h,两车间距离y(km)与乙车行驶时间x(h)之间的函数图象如 下.
下.
(1)将图中( )填上适当的值,并求甲车从A到B的速度.
(2)求从甲车返回到与乙车相遇过程中y与x的函数关系式,自变量取值范围。
(3) 求出甲车返回时行驶速度及AB两地的距离. 
(本小题满分12分)
如图,直角梯形ABCD中,AB∥DC,∠DAB=90°,AD=2DC=4,AB=6.动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与折线A-C-B的交点为Q.点M运动的时间为t(秒).
(1)当 时,求线段
时,求线段 的长;
的长;
(2)点M在线段AB上运动时,是否可以使得以C、P、Q为顶点的三角形为直角三角形,若可以,请直接写出t的值(不需解题步骤);若不可以,请说明理由.
(3)若△PCQ的面积为y,请求y关于出t 的函数关系式及自变量的取值范围;
已知反比例函数 ,下列结论不正确的是 ……………………( )
,下列结论不正确的是 ……………………( )
| A.图象必经过点(-1,3); | B. 随 随 的增大而增大; 的增大而增大; |
| C.图象位于第二、四象限内; | D.若 ,则 ,则 . . |
在平面直角坐标系内,把点 (-3,1)向右平移一个单位,则得到的对应点
(-3,1)向右平移一个单位,则得到的对应点 的坐标是( )
的坐标是( )
| A.(-3,2); | B.(-3,0); | C.(-4,1); | D.(-2,1). |
在 中,点
中,点 、
、 、
、 分别在
分别在 、
、 、
、 上,且
上,且 ,
, ,则下列三种说法:
,则下列三种说法:
①如果 ,那么四边形
,那么四边形 是矩形;
是矩形;
②如果 平分
平分 ,那么四边形
,那么四边形 是菱形;
是菱形;
③如果 且
且 ,那么四边形
,那么四边形 是菱形.
是菱形.
其中正确的有 ………………………………………( )
| A.3个; | B.2个; | C.1个; | D.0个. |

在 中,
中, ,且两边长分别为4
,且两边长分别为4 和5
和5 ,若以点
,若以点 为圆心,3
为圆心,3 为半径作⊙
为半径作⊙ ,以点
,以点 为圆心,2
为圆心,2 为半径作⊙
为半径作⊙ ,则⊙
,则⊙ 和⊙
和⊙ 位置关系是………( )
位置关系是………( )
| A.只有外切一种情况; | B.只有外离一种情况; |
| C.有相交或外切两种情况; | D.有外离或外切两种情况. |
为了解居民节约用水的情况,小丽对某个单元的住户用水量进行调查,右表是某
个单元的住户3月份用水量的调查结果。根据表中所提供的信息,这12户居民月用水量的
众数是 .
如图,E、F是矩形ABCD对角线AC上的两点,试添加一个条件:___________,
使得△ADF≌△CBE.
如图,光源P在横杆AB的上方,AB在灯光下的影子为CD,AB∥CD,已知AB
=2m,CD=6m,点P到CD的距离是2.7m,那么AB与CD间的距离是________m.
如图,已知边长为3的等边三角形ABC纸片,点E在AC边上,点F在AB边上,沿着EF折叠,使点A落在BC边上的点D的位置,且 ,则CE的长是 .
,则CE的长是 .
“校园手机”现象越来越受到社会的关注.小丽在“统计实习”活动中随机调查了学校若干名学生家长对“中学生带手机到学校”现象的 看法,统计整理并制作了如下的统计图:
看法,统计整理并制作了如下的统计图: 
(1)求这次调查的家长总数及家长表示“无所谓”的人数,并补全图①;
(2)求图②中表示家长“无所谓”的圆心角的度数;
(3)从这次接受调查的家长中,随机抽查一个,恰好是“不赞成”态度的家长的概率是多少?
如图, 、
、 两地被一大山阻隔,汽车从
两地被一大山阻隔,汽车从 地到
地到 地须经过
地须经过 地中转.为了促进
地中转.为了促进 、
、 两地的经济发展,现计划开通隧道,使汽车可以直接从
两地的经济发展,现计划开通隧道,使汽车可以直接从 地到
地到 地.已知
地.已知 ,
, ,
, 千米.若汽车的平均速度为45千米/时,则隧道开通后,汽车直接从
千米.若汽车的平均速度为45千米/时,则隧道开通后,汽车直接从 地到
地到 地需要多长时间?(参考数据:
地需要多长时间?(参考数据: )
)
如图,在直角梯形ABCD中,AD∥BC,∠A=90o,BD⊥DC,BC=10cm,CD=6cm.在线段 、
、 上有动点
上有动点 、
、 ,点
,点 以每秒
以每秒 的速度,在线段
的速度,在线段 上从点B向点C匀速运动;同时点
上从点B向点C匀速运动;同时点 以每秒
以每秒 的速度,在线段
的速度,在线段 上从点C向点D匀速运动.当点
上从点C向点D匀速运动.当点 到达点C时,点
到达点C时,点 同时停止运动.设点
同时停止运动.设点 运动的时间为t(秒).
运动的时间为t(秒).
(1)求AD的长;
(2)设四边形BFED的面积为 ,求y 关于t的函数关系式,并写出函数定义域;
,求y 关于t的函数关系式,并写出函数定义域;
(3)点 、
、 在运动过程中,如
在运动过程中,如 与
与 相似,求线段
相似,求线段 的长.
的长.
如果点(-a,-b)在反比例函数 的图象上,那么下列各点中,在此图象上的
的图象上,那么下列各点中,在此图象上的
是( )
| A.(a,b) | B.(b,-a) | C.(-a,b) | D.(-b,a) |
如图是甲、乙两位同学数学考试成绩的折线统计图,则这四次数学考试成绩( ▲ )
| A.乙成绩比甲成绩稳定 |
| B.甲成绩比乙成绩稳定 |
| C.甲、乙两人成绩一样稳定 |
| D.不能比较两人成绩的稳定性 |
今年3月26日20:30至21:30,在参与“地球一小时”活动中,南京全城节约用电约10万度.约可以减少二氧化碳排放量99700千克,这个排放量用科学记数法表示为 ▲ 千克.
在一个不透明的盒子中装有8个白球,x个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球,它是白球的概率为 ,则x= ▲ .
,则x= ▲ .
某展览大厅有3个入口和2个出口,其示意图如下.参观者从任意一个入口进入,参观结束后从任意一个出口离开.
(1)小明从进入到离开,对于入口和出口的选择有多少种不同的结果(要求画出树状图)?
(2)小明从入口1进入并从出口A离开的概率是多少?
已知:如图,△ABC中,AB=AC,BD、CE分别是AC、AB边上的高,连接DE.
求证:(1)△ABD≌△ACE;
(2)四边形BCDE是等腰梯形.
为 了了解某校九年级学生英语口语测试成绩情况,从中抽取部分学生的英语口语测试成绩统计如下图.现知道抽取的成绩中有12个满分(24分为满分).
了了解某校九年级学生英语口语测试成绩情况,从中抽取部分学生的英语口语测试成绩统计如下图.现知道抽取的成绩中有12个满分(24分为满分).

(1)抽取了 ▲ 名学生的成绩;
(2)求所抽取的成绩的均分;
(3)已知该校九年级共有6 50名学生,请估计该校九年级英语口语测试成绩在22分以上
50名学生,请估计该校九年级英语口语测试成绩在22分以上
(不含22分)的人数.
如图,二次函数y=ax2+bx的图象经过点A(4,0)、B(2,2),连结OB、AB.

(1)求a, b;
(2 )将△OAB绕点O按顺时针方向旋转135°得到△
)将△OAB绕点O按顺时针方向旋转135°得到△ ,则线段
,则线段 的中点P的坐标为 ▲ ,并判断点P是否在此二次函数的图象上,说明你的理由.
的中点P的坐标为 ▲ ,并判断点P是否在此二次函数的图象上,说明你的理由.
如图,为了测量山坡AQ上的小树BC(竖直向上)的高,测得坡角∠PAQ为30°,坡面距离AB为 10米,并测得视线AC与坡面AB的夹角为20°.求小树的高BC.(参考数据:
10米,并测得视线AC与坡面AB的夹角为20°.求小树的高BC.(参考数据:
 ,
, ,
, .精确到0.1米)
.精确到0.1米)
如图,△ABC中,AB=4,AC= 2,BC=2,以BC为直径的半圆交AB于点D,以A为圆心,AC为半径的扇形交AB于点E.
2,BC=2,以BC为直径的半圆交AB于点D,以A为圆心,AC为半径的扇形交AB于点E.

(1)以BC为直径的圆与AC所在的直线有何位置关系?请说明理由;
(2)求图中阴影部分的面积(结果可保留根号和 ).
).
如图,要建一个面积为 的长方形养鸡场(分为两个区域),养鸡场的一边靠着一面长为
的长方形养鸡场(分为两个区域),养鸡场的一边靠着一面长为 的墙,另几条边用总长为
的墙,另几条边用总长为 的竹篱笆围成,每块区域的前面各开一个宽
的竹篱笆围成,每块区域的前面各开一个宽 的门.
的门. 求这个养鸡场的长与宽.
求这个养鸡场的长与宽.
我们通常可以对一些图形进行剪切,并利用图形的轴对称、平移、旋转等进行图案设计,如图1中,可以沿线段AE剪切矩形ABCD,再将△ABE通过变换与梯形
AECD拼接成等腰梯形.请按下列要求进行图案设计:
(1)把矩形剪切2次拼接成一个菱形,请在图2中画出剪切线,再画出拼接示意图;
(2)把矩形剪切1次拼接成一个菱形,请在图3中画出剪切线,再画出拼接示意图.


(8分 )A、B两
)A、B两 地相距630千米,客车、货车分别从A、B两地同时出发,匀速相向行驶.货车两小时可到达途中C站,客车需9小时到达C站(如图1所示).货车的速度是客车的
地相距630千米,客车、货车分别从A、B两地同时出发,匀速相向行驶.货车两小时可到达途中C站,客车需9小时到达C站(如图1所示).货车的速度是客车的 ,客、货车到C站的距离分别为y1、y2(千米),它们与行驶时间x(小
,客、货车到C站的距离分别为y1、y2(千米),它们与行驶时间x(小
时)之间的函数关系如图2所示.

(1)求客、货两车的速度;
(2)求两小时后,货车到C站的距离y2与行驶时间x之间的函数关系式;
(3)如图2,两函数图象交于点E,求E点坐标,并说明它所表示的实际意义.
 的结果是……………………………………………………( )
的结果是……………………………………………………( ) ;
; ;
; ;
; .
.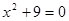 ;
; ;
;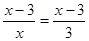 ;
;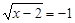 .
. .
. ,
, ,则
,则 .
. .
. 的解是 .
的解是 . 的定义域是 .
的定义域是 . 为对称轴,且在对称轴右侧部分是下降的抛物线的表
为对称轴,且在对称轴右侧部分是下降的抛物线的表 ,则这个正多边形的边数是________.
,则这个正多边形的边数是________. =
= ,
, =
= ,那么
,那么 =________.
=________.
 .
. 并把解集在数轴上表示出来.
并把解集在数轴上表示出来.
 是⊙
是⊙ 的弦,点D是弧AB的中点,过B作A
的弦,点D是弧AB的中点,过B作A B的垂线交AD的延长线于C.求证:AD=DC.
B的垂线交AD的延长线于C.求证:AD=DC.
 表示 ( ▲ )
表示 ( ▲ ) 的相反数
的相反数 的相反数
的相反数 的相反数
的相反数 的相反数
的相反数 =a6
=a6
 开平方的结果是( ▲ )
开平方的结果是( ▲ )



 中,自变量x的取值范围是 ▲ .
中,自变量x的取值范围是 ▲ . = ▲ .
= ▲ . 和⊙
和⊙ 的半径分别为3cm和5cm,且它们内切,则
的半径分别为3cm和5cm,且它们内切,则 等于 ▲ cm.
等于 ▲ cm.

 .
.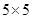 的正方形网格中,以AB为边画直角△ABC,使点C在格点上,满足这样条件的点C共 ▲ 个.
的正方形网格中,以AB为边画直角△ABC,使点C在格点上,满足这样条件的点C共 ▲ 个.
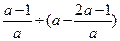 .
. ,并写出不等式组的整数解.
,并写出不等式组的整数解.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号