(本小题满分10分)
甲乙两车同时从A地出发,以各自的速度匀速向B地行驶.甲车先到达B地,停留一小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为60km/h，两车间距离y(km)与乙车行驶时间x(h)之间的函数图象如
下.
(1)将图中（ ）填上适当的值，并求甲车从A到B的速度.
(2)求从甲车返回到与乙车相遇过程中y与x的函数关系式，自变量取值范围。
(3) 求出甲车返回时行驶速度及AB两地的距离.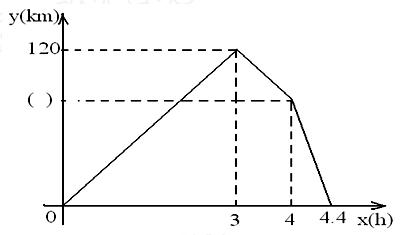 
相关试题
如图，点B的坐标为（4，3），过点B作x轴的垂线垂足为A，交反比例函数
(x>0)图象于点C；连结OB交反比例函数(x>0) 图象于点D，已知BC∶AB=2∶3。
（1）求k的值
（2）求点D的坐标。
．
如图所示．P是⊙O外一点．PA是⊙O的切线．点A是切点．B是⊙O上一点．
且PA = PB，连接AO、BO、PO、AB，并延长BO与切线PA相交于点C．
（1）求证：PB是⊙O的切线 ；
（2）求证： AC · PC=" OC" · BC ；
（3）设∠AOC =
，若cos=
，OC =" 15" ，求AB的长。
经过点A、B ．
相关知识点
推荐套卷
粤公网安备 44130202000953号