2010年高级中等学校招生全国统一考试数学卷(江苏常州)
为了迎接扬州烟花三月经贸旅游节,某学校计划由七年级(1)班的3个小组(每个小组人数都相等)制作240面彩旗.后因一个小组另有任务,改由另外两个小组完成制作彩旗的任务,这样这两个小组的每一名学生就要比原计划多做4面彩旗.如果每名学生制作彩旗的面数相等,那么每个小组有多少学生?
如图,四边形ABCD是菱形,点G是BC延长线上一点,连接AG,分别交BD、CD于点E、F,连接CE.
(1)求证:∠DAE=∠DCE;
(2)当AE=2EF时,判断FG与EF有何等量关系?并证明你的结论?
如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1:,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:≈1.414,≈1.732)
如图,在△ABC中,AB=AC,以AB为直径的半圆O交BC于点D,DE⊥AC,垂足为E.
(1)求证:点D是BC的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论;
(3)如果⊙O的直径为9,cosB=,求DE的长.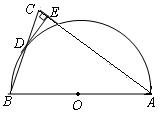
我国青海省玉树地区发生强烈地震以后,国家立即启动救灾预案,积极展开灾区运送救灾物资和对伤员的救治工作.已知西宁机场和玉树机场相距800千米,
乙两机沿同一航线各自从西宁、玉树出发,相向而行.如图,线段AB、CD分别表示甲、乙
两机离玉树机场的距离S(百千米)和所用去的时间t(小时)之间的函数关系的图象(注:
为了方便计算,将平面直角坐标系中距离S的单位定为(百千米)).观察图象回答下列问题:
(1)乙机在甲机出发后几小时,才从玉树机场出发?甲、乙两机的飞行速度每小时各为多少千米?
(2)求甲、乙两机各自的S与t的函数关系式;
(3)甲、乙两机相遇时,乙机飞行了几小时?离西宁机场多少千米?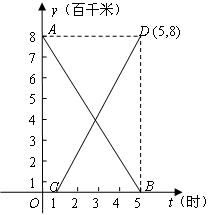
在△ABC中,∠C=90°,AC=3,BC=4,CD是斜边AB上的高,点E在斜边AB上,过点E作直线与△ABC的直角边相交于点F,设AE=x,△AEF的面积为y.
(1)求线段AD的长;
(2)若EF⊥AB,当点E在线段AB上移动时,
①求y与x的函数关系式(写出自变量x的取值范围)
②当x取何值时,y有最大值?并求其最大值;
(3)若F在直角边AC上(点F与A、C两点均不重合),点E在斜边AB上移动,试问:是否存在直线EF将△ABC的周长和面积同时平分?若存在直线EF,求出x的值;若不存在直线EF,请说明理由.
下列事件中,不可能发生的事件是 ( ).
| A.今天是星期二,明天是星期三; |
| B.打开电视,正在播放《新闻联播》; |
| C.从装有5个红球,3个蓝球的口袋中,摸出3个白球; |
| D.我们班级的同学将来会出现一位科学家. |
下面给出的五个角,可以用一副三角尺画出来的是 ( ).
(1)15°的角 (2)65º的角(3)75º的角 (4)135º的角 (5)145º的角
| A.(1)(2)(4); | B.(1)(3)(5); | C.(2)(4)(5) | D.(1)(3)(4) |
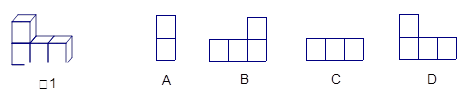
下列说法错误的是 ( ).
| A.长方体、正方体都是棱柱 | B.球体的三种视图均为同样大小的图形 |
| C.三棱柱的侧面是三角形 | D.六棱柱有六条棱、六个侧面、侧面为长方形 |
甲乙两人完成一项工作,已知甲单独做需4小时完成,乙单独做需6小时完成,若甲乙两人合作完成,需要的时间是 ( )
| A.10小时 | B.5 小时 | C.2.4 小时 | D.不能确定 |
2010年,中国成功举办了“上海世博会”,参观的人数约为70 000 000人次,用科学记数法表示70 000 000 =
如图,已知线段 与
与 两点,
两点,
① 过P点画出线段 的垂线
的垂线 ;
; ② 过Q点画出线段
② 过Q点画出线段 的平行线
的平行线 ;
;
③ 则有 .
.
(在横线上填入适当的数学符号,保留作图痕迹,不写画法)
吸烟有害健康!你知道吗,即使被动吸烟也大大危害健康.
有消息称,我国准备从2011年元月一日起在公众场所实行“禁烟”,为配合“禁烟”行动,某校组织同学们在某社区开展了“你支持哪种戒烟方式”的问卷调查,征求市民的意见,并将调查结果整理后制成了如下统计图:
根据统计图解答:
(1)同学们一共随机调查了多少人?
(2)请你把统计图补充完整;
(3)如果在该社区随机咨询一位市民,那么该市民支持“强制戒烟”的概率是多少?假定该 社区有1万人,请估计该地区大约有多少人支持“警示戒烟”这种方式.
社区有1万人,请估计该地区大约有多少人支持“警示戒烟”这种方式.
用激光测距仪测得两座山峰之间的距离为14000000米,将14000000用科学计数法表示为( )
| A.14×107 | B.14×106 | C.1.4×10 7 | D.0.14×108 |
若两圆的半径为别为2和3,圆心距为5,则两圆的位置关系为( )
| A.外离 | B.外切 | C.相交 | D.内切 |
某一公司共有51名员工(包括经理),经理的工资高于其他员工的工资,今年经理的工资从去年的200000元增加到225000元,而其他员工的工资同去年一样,这样,这家公司所有员工今年工资的平均数和中位数与去年相比将会( )
| A.平均数和中位数不变 | B.平均数增加,中位数不变 |
| C.平均数不变,中位数增加 | D.平均数和中位数都增大 |
如图,一次函数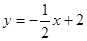 的图象上有两点A、B,A点的横坐标为2,B点的横坐标为a(0<a<4且a≠2),过点A、B分别作x轴的垂线,垂足为C、D,△AOC、△BOD的面积分别为S1、S2,S1与S2的大小关系是( )
的图象上有两点A、B,A点的横坐标为2,B点的横坐标为a(0<a<4且a≠2),过点A、B分别作x轴的垂线,垂足为C、D,△AOC、△BOD的面积分别为S1、S2,S1与S2的大小关系是( )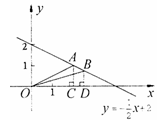
A.S1>S2
B.S1=S2
C.S1<S2
D.无法确定
一次考试中7名学生的成绩(单位:分)如下:61,62,71,78,85,85,92,这7名学生的成绩的极差是 分,众数是 分
如图,AB是⊙O的直径,弦DC与AB相交于点E,若∠ACD=60°,∠ADC=50°,则∠ABD= °,∠CEB= °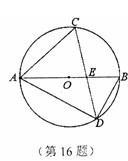
如图,圆圈内分别有0,1,2,3,4,…,11这12个数字。电子跳蚤每跳一次,可以从一个圆圈跳到相邻的圆圈,现在,一只电子跳蚤从标有数字“0”的圆圈开始,按逆时针方向跳了2010次后,落在一个圆圈中,该圆圈所标的数字是 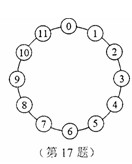
(本小题满分7分)
某中学七年级(8)班同学全部参加课外体育活动情况统计如图:
(1)请你根据以上统计图中的信息,填写下表:
| 该班人数 |
这五个活动项目人数的中位数 |
这五个活动项目人数的平均数 |
| |
|
|
(2)请你将该条形统计图补充完整
(本小题满分8分)
如图所示,小吴和小黄在玩转盘游戏,准备了两个可以自由转动的转盘甲、乙,每个转盘被分成面积相等的几个扇形区域,并在每个扇形区域内标上数字,游戏规则:同时转动两个转盘,当转盘停止转动后,指针所指扇形区域内的数字之和为4,5或6时,则小吴胜;否则小黄胜。(如果指针恰好指在分割线上,那么重转一次,直到指针指向某一扇形区域为止)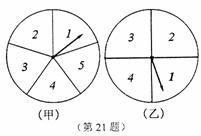
(1)这个游戏规则对双方公平吗?说说你的理由;
(2)请你设计一个对双方都公平的游戏规则。
(本小题满分5分)
如图,在△ABC中,点D、E分别在边AC、AB上,BD=CE,∠DBC=∠ECB。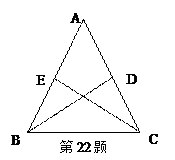
求证:AB=AC
(本小题满分7分)
如图,在△ABC中,AB=AC,D为BC中点。四边形ABDE是平行四边形。
求证:四边形ADCE是矩形
(本小题满分7分)
如图,在△ABC和△CDE中,AB=AC=CE,BC=DC=DE,AB>BC,∠BAC=∠DCE=∠a,点B、C、D在直线l上,按下列要求画图(保留画图痕迹):
(1)画出点E关于直线l的对称点E′,连接CE′、DE′;
(2)以点C为旋转中心,将(1)中所得△CDE′按逆时针方向旋转,使得CE′与CA重合,得到△CD′E″(A)。画出△CD′E″(A),并解决下面问题:
①线段AB和线段CD′的位置关系是 ,理由是:
②求∠a的度数。
(本小题满分6分)
小明在研究了苏科版《有趣的坐标系》后,得到启发,针对正六边形OABCDE,自己设计了一个坐标系如图。该坐标系以O为原点,直线OA为x轴,以正六边形OABCDE的边长为一个单位长。坐标系中的任意一点P用一有序实数对(a,b)来表示,我们称这个有序实数对(a,b)为P点的坐标。坐标系中点的坐标的确定方法如下: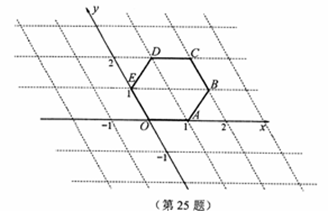
(1)x轴上点M的坐标为(m,0),其中m为M在x轴上表示的实数;
(2)y轴上点N的坐标为(0,n),其中n为N点在y轴上表示的实数;
(3)不在x、y轴上的点Q的坐标为(a,b),其中a为过点Q且与y轴平行的直线与x轴的交点在x轴上表示的实数,b为过点Q且与x轴平行饿直线与y轴的交点在y轴上表示的实数。
则:(1)分别写出点A、B、C的坐标;
(2)标出点M(2,3)的位置;
(3)若点K(x,y)为射线OD上任一点,求x与y所满足的关系式
向阳花卉基地出售两种花卉--百合和玫瑰,其单价为:玫瑰4元/株,百合5元/株,如果同一客户所购的玫瑰数量大于1200株,那么每株玫瑰还可降价1元。现某鲜花店向向阳花卉基地采购玫瑰1000株~1500株,百合若干株,此鲜花店本次用于采购玫瑰和百合恰好花去了9000元。然后再以玫瑰5元、百合6.5元的价格卖出。问:此鲜花店应如何采购这两种鲜花才能使获得的毛利润最大?
(注:1000株~1500株,表示大于或等于1000株,且小于或等于1500株。毛利润=鲜花店卖出百合和玫瑰所获的总金额-购进百合和玫瑰的所需的总金额)
(本小题满分9分)
如图,已知二次函数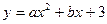 的图象与x轴相交于点A、C,与y轴交于点B,A(
的图象与x轴相交于点A、C,与y轴交于点B,A(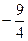 ,0),且△AOB~△BOC。
,0),且△AOB~△BOC。
(1)求C点坐标、∠ABC的度数及二次函数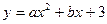 的关系式;
的关系式;
(2)在线段AC上是否存在点M(m,0),使得以线段BM为直径的圆与边BC交于P点(与点B不同),且以点P、C、O为顶点的三角形是等腰三角形?若存在,求出m的值;若不存在,请说明理由




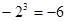
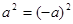
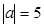 ,
,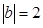 ,那么
,那么 的值一定是 ( ).
的值一定是 ( ).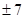 或
或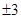
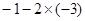 =
= 
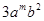 与
与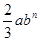 是同类项,则
是同类项,则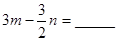
 互为相反数,则
互为相反数,则 =___
=___ 
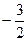 和它们的相反数的点
和它们的相反数的点

 其中
其中

 的图象经过的点是( )
的图象经过的点是( ) ,2)
,2)




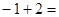 ,
,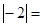 ,
,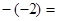 ,
,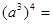 。
。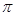 ㎝2,则扇形的圆心角是 ,扇形的弧长是 ㎝(结果保留
㎝2,则扇形的圆心角是 ,扇形的弧长是 ㎝(结果保留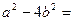
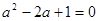 ,则
,则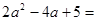
 ;
; 
 ;
; 

 粤公网安备 44130202000953号
粤公网安备 44130202000953号