2022年中考数学专题:图形的变化(二)
以下四个标志,每个标志都有图案和文字说明,其中的图案是轴对称图形是
| A. |
|
B. |
|
| C. |
|
D. |
|
将一张三角形纸片按如图步骤①至④折叠两次得图⑤,然后剪出图⑤中的阴影部分,则阴影部分展开铺平后的图形是

| A. |
等腰三角形 |
B. |
直角三角形 |
C. |
矩形 |
D. |
菱形 |
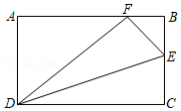
如图,在矩形 中, , ,点 为 上一点,把 沿 翻折,点 恰好落在 边上的 处,则 的长是
| A. |
1 |
B. |
|
C. |
|
D. |
|
对称美是美的一种重要形式,它能给与人们一种圆满、协调和平的美感,下列图形属于中心对称图形的是
| A. |
|
B. |
|
C. |
|
D. |
|
如图, 的顶点 , ,点 在 轴的正半轴上,延长 交 轴于点 .将 绕点 顺时针旋转得到△ ,当点 的对应点 落在 上时, 的延长线恰好经过点 ,则点 的坐标为

| A. |
, |
B. |
, |
C. |
, |
D. |
, |
如图, ,以 为圆心,4为半径作弧交 于点 ,交 于点 ,分别以点 , 为圆心,大于 的长为半径画弧,两弧在 的内部相交于点 ,画射线 交 于点 , 为 上一动点,连接 , ,则阴影部分周长的最小值为 .

已知菱形 的面积为 ,点 是一边 上的中点,点 是对角线 上的动点.连接 ,若 平分 ,则线段 与 的和的最小值为 ,最大值为 .
如图,三角形纸片 中,点 , , 分别在边 , , 上, , ,将这张纸片沿直线 翻折,点 与点 重合.若 , ,则四边形 的面积为 .
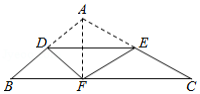
如图,在 中, , , ,点 在线段 上,且 , 是线段 上的一点,连接 ,把四边形 沿直线 翻折,得到四边形 ,当点 恰好落在线段 上时, .

已知抛物线 与 轴交于 , 两点(点 在点 的左侧)与 轴交于点 ,点 在抛物线上, 是该抛物线对称轴上一动点,当 的值最小时, 的面积为 .
将一副三角板如图放置在平面直角坐标系中,顶点 与原点 重合, 在 轴正半轴上,且 ,点 在 上, ,将这副三角板整体向右平移 个单位, , 两点同时落在反比例函数 的图象上.

在平面直角坐标系 中, 的半径为1.对于点 和线段 ,给出如下定义:若将线段 绕点 旋转可以得到 的弦 , 分别是 , 的对应点),则称线段 是 的以点 为中心的“关联线段”.
(1)如图,点 , , , , , , 的横、纵坐标都是整数.在线段 , , 中, 的以点 为中心的“关联线段”是 ;
(2) 是边长为1的等边三角形,点 ,其中 .若 是 的以点 为中心的“关联线段”,求 的值;
(3)在 中, , .若 是 的以点 为中心的“关联线段”,直接写出 的最小值和最大值,以及相应的 长.

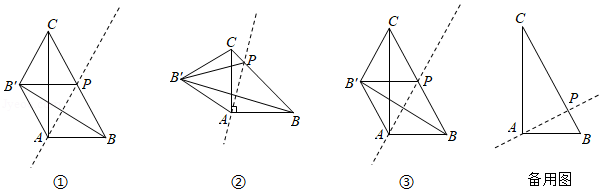
如图,在 中,点 为斜边 上一动点,将 沿直线 折叠,使得点 的对应点为 ,连接 , , , .
(1)如图①,若 ,证明: .
(2)如图②,若 , ,求 的值.
(3)如图③,若 ,是否存在点 ,使得 .若存在,求此时 的值;若不存在,请说明理由.
如图,在平面直角坐标系中, 的顶点坐标分别是 , , .
(1)将 以 为旋转中心旋转 ,画出旋转后对应的△ ;
(2)将 平移后得到△ ,若点 的对应点 的坐标为 ,求△ 的面积.

实践与探究
操作一:如图①,已知正方形纸片 ,将正方形纸片沿过点 的直线折叠,使点 落在正方形 的内部,点 的对应点为点 ,折痕为 ,再将纸片沿过点 的直线折叠,使 与 重合,折痕为 ,则 度.
操作二:如图②,将正方形纸片沿 继续折叠,点 的对应点为点 .我们发现,当点 的位置不同时,点 的位置也不同.当点 在 边的某一位置时,点 恰好落在折痕 上,则 度.
在图②中,运用以上操作所得结论,解答下列问题:
(1)设 与 的交点为点 .求证: ;
(2)若 ,则线段 的长为 .

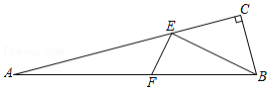
如图,在 中, , , 为 的中点,点 在 上,以点 为中心,将线段 顺时针旋转 得到线段 ,连接 , .
(1)比较 与 的大小;用等式表示线段 , , 之间的数量关系,并证明;
(2)过点 作 的垂线,交 于点 ,用等式表示线段 与 的数量关系,并证明.

学习了图形的旋转之后,小明知道,将点 绕着某定点 顺时针旋转一定的角度 ,能得到一个新的点 ,经过进一步探究,小明发现,当上述点 在某函数图象上运动时,点 也随之运动,并且点 的运动轨迹能形成一个新的图形.
试根据下列各题中所给的定点 的坐标、角度 的大小来解决相关问题.
【初步感知】
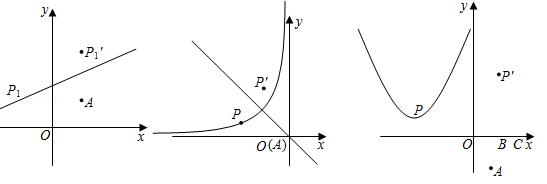
如图1,设 , ,点 是一次函数 图象上的动点,已知该一次函数的图象经过点 .
(1)点 旋转后,得到的点 的坐标为 ;
(2)若点 的运动轨迹经过点 ,求原一次函数的表达式.
【深入感悟】
如图2,设 , ,点 是反比例函数 的图象上的动点,过点 作二、四象限角平分线的垂线,垂足为 ,求 的面积.
【灵活运用】
如图3,设 , ,点 是二次函数 图象上的动点,已知点 、 ,试探究 的面积是否有最小值?若有,求出该最小值;若没有,请说明理由.
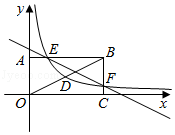
如图,在平面直角坐标系中,矩形 的两边 、 分别在坐标轴上,且 , ,连接 .反比例函数 的图象经过线段 的中点 ,并与 、 分别交于点 、 .一次函数 的图象经过 、 两点.
(1)分别求出一次函数和反比例函数的表达式;
(2)点 是 轴上一动点,当 的值最小时,点 的坐标为 .
如图,在 的方格纸中,线段 的端点均在格点上,请按要求画图.

(1)如图1,画出一条线段 ,使 , 在格点上;
(2)如图2,画出一条线段 ,使 , 互相平分, , 均在格点上;
(3)如图3,以 , 为顶点画出一个四边形,使其是中心对称图形,且顶点均在格点上.
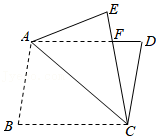
如图,点 为正方形 外一点, ,将 绕 点逆时针方向旋转 得到 , 的延长线交 于 点.
(1)试判定四边形 的形状,并说明理由;
(2)已知 , ,求 的长.

 节能
节能 绿色环保
绿色环保 永洁环保
永洁环保 绿色食品
绿色食品


















 粤公网安备 44130202000953号
粤公网安备 44130202000953号