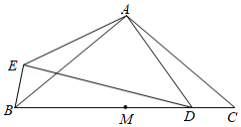
如图,在 中, , , 为 的中点,点 在 上,以点 为中心,将线段 顺时针旋转 得到线段 ,连接 , .
(1)比较 与 的大小;用等式表示线段 , , 之间的数量关系,并证明;
(2)过点 作 的垂线,交 于点 ,用等式表示线段 与 的数量关系,并证明.
相关知识点
推荐套卷
如图,在 中, , , 为 的中点,点 在 上,以点 为中心,将线段 顺时针旋转 得到线段 ,连接 , .
(1)比较 与 的大小;用等式表示线段 , , 之间的数量关系,并证明;
(2)过点 作 的垂线,交 于点 ,用等式表示线段 与 的数量关系,并证明.
