2020年黑龙江省牡丹江市、鸡西市朝鲜族学校中考数学试卷

下列图形中，既是轴对称图形，又是中心对称图形的个数有 $($ 　　 $)$

下列运算正确的是 $($ 　　 $)$

如图是由5个立方块搭成的几何体的俯视图，小正方形中的数字表示该位置上的小立方块的个数，则这个几何体的主视图是 $($ 　　 $)$

现有两个不透明的袋子，一个装有2个红球、1个白球，另一个装有1个黄球、2个红球，这些球除颜色外完全相同，从两个袋子中各随机摸出1个球，摸出的两个球颜色相同的概率是 $($ 　　 $)$

一组数据4，4， $x$ ，8，8有唯一的众数，则这组数据的平均数是 $($ 　　 $)$

如图，在 $\mathit{\Delta ABC}$ 中， $\sin B=\frac{1}{3}$ ， $\tan C=2$ ， $\mathit{AB}=3$ ，则 $\mathit{AC}$ 的长为 $($ 　　 $)$

如图，点 $A$ ， $B$ ， $S$ 在圆上，若弦 $\mathit{AB}$ 的长度等于圆半径的 $\sqrt{2}$ 倍，则 $\angle \mathit{ASB}$ 的度数是 $($ 　　 $)$

若 $\left\{\begin{array}{c}a=2\\ b=1\end{array}\right.$ 是二元一次方程组 $\left\{\begin{array}{c}\frac{3}{2}\mathit{ax}+\mathit{by}=5\\ \mathit{ax}-\mathit{by}=2\end{array}\right.$ 的解，则 $x+2y$ 的算术平方根为 $($ 　　 $)$

如图，在菱形 $\mathit{OABC}$ 中，点 $B$ 在 $x$ 轴上，点 $A$ 的坐标为 $(2$ ， $2\sqrt{3})$ ，将菱形绕点 $O$ 旋转，当点 $A$ 落在 $x$ 轴上时，点 $C$ 的对应点的坐标为 $($ 　　 $)$

若关于 $x$ 的分式方程 $\frac{2}{x-1}=\frac{m}{x}$ 有正整数解，则整数 $m$ 的值是 $($ 　　 $)$

如图， $A$ ， $B$ 是双曲线 $y=\frac{k}{x}$ 上的两个点，过点 $A$ 作 $\mathit{AC}\perp x$ 轴，交 $\mathit{OB}$ 于点 $D$ ，垂足为点 $C$ ．若 $\mathit{\Delta ODC}$ 的面积为1， $D$ 为 $\mathit{OB}$ 的中点，则 $k$ 的值为 $($ 　　 $)$

如图是二次函数 $y=a{x}^2+\mathit{bx}+c(a\ne 0)$ 图象的一部分，对称轴为 $x=\frac{1}{2}$ ，且经过点 $(2,0)$ ．下列说法：

① $\mathit{abc}<0$ ；② $-2b+c=0$ ；③ $4a+2b+c<0$ ；④若 $(-\frac{5}{2}$ ， $y_1)$ ， $(\frac{5}{2}$ ， $y_2)$ 是抛物线上的两点，则 $y_1<y_2$ ；⑤ $\frac{1}{4}b>m(\mathit{am}+b)$ （其中 $m\ne \frac{1}{2})$ ．

其中说法正确的是 $($ 　　 $)$

一周时间有604800秒，604800用科学记数法表示为　   　．

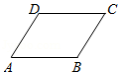
如图，在四边形$\mathit{ABCD}$中，$\mathit{AD}//\mathit{BC}$，在不添加任何辅助线的情况下，请你添加一个条件　        　，使四边形$\mathit{ABCD}$是平行四边形（填一个即可）．

在函数$y=\frac{x}{\sqrt{2x-1}}$中，自变量$x$的取值范围是　   　．

“元旦”期间，某商店单价为130元的书包按八折出售可获利$30\%$，则该书包的进价是　 　元．

将抛物线$y={(x-1)}^2-5$关于$y$轴对称，再向右平移3个单位长度后顶点的坐标是　   　．

如图是由同样大小的圆按一定规律排列所组成的，其中第1个图形中一共有4个圆，第2个图形中一共有8个圆，第3个图形中一共有14个圆，第4个图形中一共有22个圆$\dots \dots$按此规律排列下去，第9个图形中圆的个数是　 　个．

在半径为$\sqrt{5}$的$\odot O$中，弦$\mathit{AB}$垂直于弦$\mathit{CD}$，垂足为$P$，$\mathit{AB}=\mathit{CD}=4$，则$S_{\mathit{\Delta ACP}}=$　     　．

如图，正方形$\mathit{ABCD}$中，点$E$在边$\mathit{AD}$上，点$F$在边$\mathit{CD}$上，若$\angle \mathit{BEF}=\angle \mathit{EBC}$，$\mathit{AB}=3\mathit{AE}$，则下列结论：

①$\mathit{DF}=\mathit{FC}$；

②$\mathit{AE}+\mathit{DF}=\mathit{EF}$；

③$\angle \mathit{BFE}=\angle \mathit{BFC}$；

④$\angle \mathit{ABE}+\angle \mathit{CBF}=45°$；

⑤$\angle \mathit{DEF}+\angle \mathit{CBF}=\angle \mathit{BFC}$；

⑥$\mathit{DF}:\mathit{DE}:\mathit{EF}=3:4:5$；

⑦$\mathit{BF}:\mathit{EF}=3\sqrt{5}:5$．

其中结论正确的序号有　       　．

先化简，再求值：$\frac{1}{3-x}-\frac{x^2+6x+9}{x^2+3x}÷\frac{x^2-9}{2x}$，其中$x=1-2\tan 45°$．

已知抛物线$y=a{(x-2)}^2+c$经过点$A(-2,0)$和点$C(0,\frac{9}{4})$，与$x$轴交于另一点$B$，顶点为$D$．

（1）求抛物线的解析式，并写出顶点$D$的坐标；

（2）如图，点$E$，$F$分别在线段$\mathit{AB}$，$\mathit{BD}$上（点$E$不与点$A$，$B$重合），且$\angle \mathit{DEF}=\angle \mathit{DAB}$，$\mathit{DE}=\mathit{EF}$，直接写出线段$\mathit{BE}$的长．

等腰三角形$\mathit{ABC}$中，$\mathit{AB}=\mathit{AC}=4$，$\angle \mathit{BAC}=45°$，以$\mathit{AC}$为腰作等腰直角三角形$\mathit{ACD}$，$\angle \mathit{CAD}$为$90°$，请画出图形，并直接写出点$B$到$\mathit{CD}$的距离．

为了解本校学生对新闻（A）、体育（B）、动画（C）、娱乐（D）、戏曲（E）五类电视节目的喜爱情况，课题小组随机选取该校部分学生进行了问卷调查，并根据调查结果绘制了两幅不完整的统计图，请根据统计图解答下列问题：

（1）本次接受问卷调查的学生有　　名；

（2）补全条形统计图；

（3）扇形统计图中，$B$类节目所对应的扇形圆心角的度数为　　度；

（4）该校共有2000名学生，根据调查结果估计该校最喜爱新闻节目的学生数．

$A$，$B$两城市之间有一条公路相连，公路中途穿过$C$市，甲车从$A$市到$B$市，乙车从$C$市到$A$市，甲车的速度比乙车的速度慢20千米$/$时，两车距离$C$市的路程$y$（单位：千米）与驶的时间$t$（单位：小时）的函数图象如图所示，结合图象信息，解答下列问题：

（1）甲车的速度是　　千米$/$时，在图中括号内填入正确的数；

（2）求图象中线段$\mathit{MN}$所在直线的函数解析式，不需要写出自变量的取值范围；

（3）直接写出甲车出发后几小时，两车距$C$市的路程之和是460千米．

$\mathit{\Delta ABC}$中，点$D$在直线$\mathit{AB}$上．点$E$在平面内，点$F$在$\mathit{BC}$的延长线上，$\angle E=\angle \mathit{BDC}$，$\mathit{AE}=\mathit{CD}$，$\angle \mathit{EAB}+\angle \mathit{DCF}=180°$；

（1）如图①，求证$\mathit{AD}+\mathit{BC}=\mathit{BE}$；

（2）如图②、图③，请分别写出线段$\mathit{AD}$，$\mathit{BC}$，$\mathit{BE}$之间的数量关系，不需要证明；

（3）若$\mathit{BE}\perp \mathit{BC}$，$\tan \angle \mathit{BCD}=\frac{3}{4}$，$\mathit{CD}=10$，则$\mathit{AD}=$　          　．

某商场准备购进$A$、$B$两种型号电脑，每台$A$型号电脑进价比每台$B$型号电脑多500元，用40000元购进$A$型号电脑的数量与用30000元购进$B$型号电脑的数量相同，请解答下列问题：

（1）$A$，$B$型号电脑每台进价各是多少元？

（2）若每台$A$型号电脑售价为2500元，每台$B$型号电脑售价为1800元，商场决定同时购进$A$，$B$两种型号电脑20台，且全部售出，请写出所获的利润$y$（单位：元）与$A$型号电脑$x$（单位：台）的函数关系式，若商场用不超过36000元购进$A$，$B$两种型号电脑，$A$型号电脑至少购进10台，则有几种购买方案？

（3）在（2）问的条件下，将不超过所获得的最大利润再次购买$A$，$B$两种型号电脑捐赠给某个福利院，请直接写出捐赠$A$，$B$型号电脑总数最多是多少台．

如图，在平面直角坐标系中，四边形$\mathit{OABC}$的边$\mathit{OC}$在$x$轴上，$\mathit{OA}$在$y$轴上．$O$为坐标原点，$\mathit{AB}//\mathit{OC}$，线段$\mathit{OA}$，$\mathit{AB}$的长分别是方程$x^2-9x+20=0$的两个根$(\mathit{OA}<\mathit{AB})$，$\tan \angle \mathit{OCB}=\frac{4}{3}$．

（1）求点$B$，$C$的坐标；

（2）$P$为$\mathit{OA}$上一点，$Q$为$\mathit{OC}$上一点，$\mathit{OQ}=5$，将$\mathit{\Delta POQ}$翻折，使点$O$落在$\mathit{AB}$上的点$O\text{'}$处，双曲线$y=\frac{k}{x}$的一个分支过点$O\text{'}$．求$k$的值；

（3）在（2）的条件下，$M$为坐标轴上一点，在平面内是否存在点$N$，使以$O\text{'}$，$Q$，$M$，$N$为顶点四边形为矩形？若存在，请直接写出点$N$的坐标；若不存在，请说明理由．