为了解本校学生对新闻（A）、体育（B）、动画（C）、娱乐（D）、戏曲（E）五类电视节目的喜爱情况，课题小组随机选取该校部分学生进行了问卷调查，并根据调查结果绘制了两幅不完整的统计图，请根据统计图解答下列问题：
（1）本次接受问卷调查的学生有 名；
（2）补全条形统计图；
（3）扇形统计图中，类节目所对应的扇形圆心角的度数为 度；
（4）该校共有2000名学生，根据调查结果估计该校最喜爱新闻节目的学生数．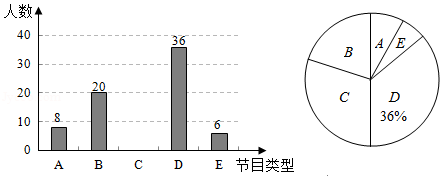
相关试题
如图，△ACD和△BCE都是等腰直角三角形，∠ACD＝∠BCE＝90°，AE交DC于F，BD分别交CE，AE于点G、H试猜测线段AE和BD数量关系，并说明理由
如图，在△ABC中，AB=AC，∠ABC=72°．
(1)用直尺和圆规作∠ABC的平分线BD交AC于点D（保留作图痕迹，不要求写作法）；
(2)在(1)中作出∠ABC的平分线BD后，求∠BDC的度数．
轴正半轴上一点，⊙M与
的两根，ON是⊙M的切线，N为切点，N在第四象限．
推荐套卷
粤公网安备 44130202000953号