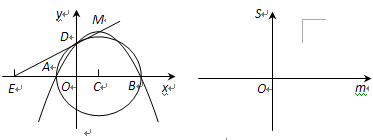
已知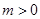 ,点
,点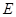 的坐标为
的坐标为 ,关于
,关于 的二次函数
的二次函数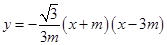 图象的顶点为
图象的顶点为 ,图象交
,图象交 轴于
轴于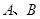 两点,交
两点,交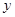 轴正半轴于
轴正半轴于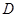 点.以
点.以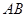 为直径作圆,其圆心为
为直径作圆,其圆心为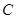 .
. 
(1)写出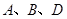 三点的坐标(可用含
三点的坐标(可用含 的代数式表示);
的代数式表示);
(2)当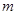 为何值时
为何值时 点在直线
点在直线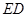 上?判定此时直线
上?判定此时直线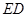 与圆的位置关系?
与圆的位置关系?
(3)连接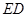 ,当
,当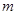 变化时,试用
变化时,试用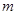 表示
表示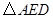 的面积
的面积 ,并在给出的直角坐标系中画出S关于m的函数图象的示意图.
,并在给出的直角坐标系中画出S关于m的函数图象的示意图.
相关知识点
推荐套卷
已知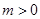 ,点
,点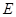 的坐标为
的坐标为 ,关于
,关于 的二次函数
的二次函数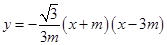 图象的顶点为
图象的顶点为 ,图象交
,图象交 轴于
轴于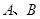 两点,交
两点,交 轴正半轴于
轴正半轴于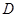 点.以
点.以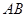 为直径作圆,其圆心为
为直径作圆,其圆心为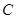 .
. 
(1)写出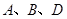 三点的坐标(可用含
三点的坐标(可用含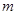 的代数式表示);
的代数式表示);
(2)当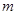 为何值时
为何值时 点在直线
点在直线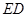 上?判定此时直线
上?判定此时直线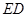 与圆的位置关系?
与圆的位置关系?
(3)连接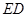 ,当
,当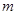 变化时,试用
变化时,试用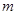 表示
表示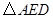 的面积
的面积 ,并在给出的直角坐标系中画出S关于m的函数图象的示意图.
,并在给出的直角坐标系中画出S关于m的函数图象的示意图.